Question

用min{a，b}表示a，b两数中的最小值，即min{a，b}=

a    a≤b b    a＞b

，若函数f（x）=min{|x|，|x+t|}的图象关于直线x=-

1

2

对称，则函数y=f（x）-c图象与x轴有4个不同的交点，则实数c的取值范围（　　）

• A、(0，

  1

  2

  )
• B、(0，

  1

  2

  )∪(

  1

  2

  ，+∞)
• C、（0，1）
• D、（0，1）∪（1，+∞）

Answer 1

分析：根据新定义，利用对称性下确定t的值，然后 将函数转化为两个图象的交点问题，利用数形结合即可得到结论．

解答：解：∵min{a，b}表示a，b两数中的最小值，
∴当x=0时，y=min{|x|，|x+t|}=|0|=0，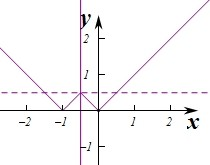
∵函数y=min{|x|，|x+t|}的图象关于直线x=-

1

2

对称，
∴当x=-1时与x=0时的值相等，
即min{|-1|，|-1+t|}=|-1+t|=0，
解得t=1．
∴f（x）=min{|x|，|x+1|}，
作出函数f（x）的图象如图：
由图象可知当x=-

1

2

时，f（-

1

2

）=

1

2

，
由y=f（x）-c=0得f（x）=c．
∴要使函数y=f（x）-c图象与x轴有4个不同的交点，
则0＜c＜

1

2

，
故选：A．

点评：本题主要考查函数对称性的应用，以及函数新定义的理解，利用数形结合是解决本题的关键，考查学生的综合应用能力．