题目内容
15．已知函数f（x）=$\frac{1}{2}$（2x+2-x）；（1）求函数的定义域；
（2）判断函数的奇偶性；
（3）判断并证明函数的单调性．
分析 （1）利用指数函数，可得函数的定义域；
（2）利用函数的奇偶性的定义，可得结论；
（3）利用导数的正负，即可判断并证明函数的单调性．
解答 解：（1）函数的定义域为R；
（2）f（-x）=$\frac{1}{2}$（2-x+2x）=f（x），∴函数是偶函数；
（3）∵f（x）=$\frac{1}{2}$（2x+2-x），
∴f′（x）=$\frac{1}{2}$（2x-2-x）•ln2
∴x＞0，f′（x）＞0；x＜0，f′（x）＜0．
∴函数在[0，+∞）上单调递增，在（-∞，0）上单调递减．
点评 本题考查函数的单调性、奇偶性，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
通城学典默写能手系列答案
相关题目
6．对定义在R上的函数f（x），若实数x0满足f（x0）=x0，则x0称为f（x）的一个不动点．设二次函数f（x）=x2+mx-m+2，若f（x）在[0，+∞）上有不动点，则m的取值范围是（ ）
| A． | [-1-2$\sqrt{2}$，2] | B． | （-∞，-1-2$\sqrt{2}$]∪[2，+∞） | C． | [-1，2] | D． | （-∞，-1]∪[2，+∞） |
3．函数f（x）=$\frac{{a}^{x+1}+{b}^{x+1}}{{a}^{x}+{b}^{x}}$（a＞0，b＞0，a≠b）在R上的单调性为（ ）
| A． | 增函数 | B． | 减函数 | C． | 不增不减函数 | D． | 与a，b的取值有关 |
10．直角坐标系中，方程|x|•y=1表示的曲线是（ ）
| A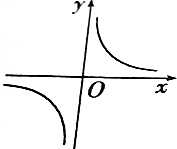． |  | B． |  | ||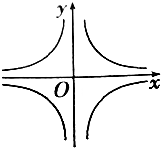
| C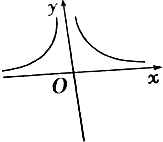． |  | D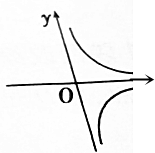． |  |