题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,
,![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)借助题设条件运用导数的几何意义建立方程求解;(2)借助题设运用转化化归的思想进行转化再运用导数知识求解;(3)依据题设先将问题进行转化,再借助导数知识分类整合思想分类探求求解.
试题解析:
(1)由![]()
![]() ,得
,得![]() ,
,
由题意![]() ,所以
,所以![]() .
.
(2)![]() ,
,
因为对任意两个不等的正数![]() ,
,![]() ,都有
,都有![]() ,
,
设![]() ,则
,则![]() ,即
,即![]() 恒成立,
恒成立,
问题等价于函数![]() ,即
,即![]() 在
在![]() 为增函数,
为增函数,
所以![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() .
.
(3)不等式![]() 等价于
等价于![]() ,
,
整理得![]() ,
,
设![]() ,由题意知,在
,由题意知,在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,
,
由![]() ,
,
因为![]() ,所以
,所以![]() ,令
,令![]() ,得
,得![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
只需![]() ,解得
,解得![]() .
.
②当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 处取最小值,
处取最小值,
令![]() ,即
,即![]() ,可得
,可得![]() ,
,
考查式子![]() ,因为
,因为![]() ,可得左端大于1,而右端小于1,所以不等式不可能成立.
,可得左端大于1,而右端小于1,所以不等式不可能成立.
③当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
只需![]() ,解得
,解得![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.

【题目】班主任为了对本班学生的考试成绩进行分析,决定从本班24名女同学,18名男同学中随机抽取一个容量为7的样本进行分析.
(1)如果按照性别比例分层抽样,可以得到多少个不同的样本?(写出算式即可,不必计算出结果)
(2)如果随机抽取的7名同学的数学,物理成绩(单位:分)对应如下表:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
数学成绩 | 60 | 65 | 70 | 75 | 85 | 87 | 90 |
物理成绩 | 70 | 77 | 80 | 85 | 90 | 86 | 93 |
①若规定85分以上(包括85分)为优秀,从这7名同学中抽取3名同学,记3名同学中数学和物理成绩均为优秀的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
②根据上表数据,求物理成绩![]() 关于数学成绩
关于数学成绩![]() 的线性回归方程(系数精确到0.01);若班上某位同学的数学成绩为96分,预测该同学的物理成绩为多少分?
的线性回归方程(系数精确到0.01);若班上某位同学的数学成绩为96分,预测该同学的物理成绩为多少分?
附:线性回归方程![]() ,
,
其中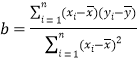 ,
,![]() .
.
|
|
|
|
76 | 83 | 812 | 526 |