题目内容
(本题10分)
已知函数 (
( 是自然对数的底数,
是自然对数的底数, ).
).
(I)证明:对 ,不等式
,不等式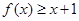 恒成立;
恒成立;
(II)数列 的前
的前 项和为
项和为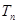 ,求证:
,求证: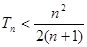 .
.
【答案】
解:(I)设
 ,当
,当 时,
时, 函数
函数 单调递增;
单调递增;
当 时,
时, ,函数
,函数 单调递减. 当
单调递减. 当 时,
时, .
.
|
|
(-∞,1) |
1 |
(1,+∞) |
|
|
- |
0 |
+ |
|
|
递减 |
极小值 |
递增 |

(II)由(I)可知,对任意的实数 ,不等式
,不等式 恒成立,设
恒成立,设
所以 ,
, ,即
,即 ,
,
 ,
,

【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 的不等式
的不等式 (Ⅰ)当
(Ⅰ)当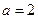 时,解不等式;
时,解不等式; 的取值范围。
的取值范围。 是奇
是奇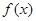 有最小值2,且f (1)
有最小值2,且f (1) .
.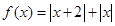
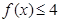 ;
;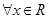 ,恒有
,恒有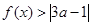 成立,求
成立,求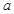 的取值范围.
的取值范围.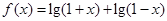
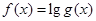 ,判断函数
,判断函数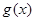 在
在 上的单调性并用定义证明
上的单调性并用定义证明