题目内容
已知命题p:不等式|x|+|x+1|>m的解集为R,命题q:f(x)=-log(3m-1)x是增函数,若p或q为真命题,p且q为假命题,则m的取值范围是 ________.
(-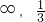 ]
] ,1)
,1)
分析:根据题设条件,先分别求出命题P和命题q,再由p或q为真命题,p且q为假命题,知“p真q假”或“p假q真”.由此能求出m的取值范围.
解答:设y=|x|+|x+1|,
由x=0和x+1=0,得x=0和x=-1.
当x≥0时,y=x+x+1=2x+1≥1,
当-1≤x<0时,y=-x+x+1=1,
当x<-1时,y=-2x-1>1,
综上所述,y≥1.
∴命题p:不等式|x|+|x+1|>m的解集为R,?命题p:m<1.
∵命题q:f(x)=-log(3m-1)x是增函数,
∴0<3m-1<1,解得命题q: .
.
∵p或q为真命题,p且q为假命题,
∴“p真q假”或“p假q真”.
当“p真q假”时, ,解得m
,解得m 或
或 .
.
当“p假q真”时, ,解为∅.
,解为∅.
综上所述,m的取值范围是(-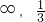 ]
] ,1).
,1).
故答案为:(-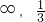 ]
] ,1).
,1).
点评:本题考查命题的真假判断和应用,解题时要认真审题,仔细解答,注意公式的合理运用.
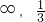 ]
] ,1)
,1)分析:根据题设条件,先分别求出命题P和命题q,再由p或q为真命题,p且q为假命题,知“p真q假”或“p假q真”.由此能求出m的取值范围.
解答:设y=|x|+|x+1|,
由x=0和x+1=0,得x=0和x=-1.
当x≥0时,y=x+x+1=2x+1≥1,
当-1≤x<0时,y=-x+x+1=1,
当x<-1时,y=-2x-1>1,
综上所述,y≥1.
∴命题p:不等式|x|+|x+1|>m的解集为R,?命题p:m<1.
∵命题q:f(x)=-log(3m-1)x是增函数,
∴0<3m-1<1,解得命题q:
 .
.∵p或q为真命题,p且q为假命题,
∴“p真q假”或“p假q真”.
当“p真q假”时,
 ,解得m
,解得m 或
或 .
.当“p假q真”时,
 ,解为∅.
,解为∅.综上所述,m的取值范围是(-
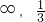 ]
] ,1).
,1).故答案为:(-
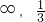 ]
] ,1).
,1).点评:本题考查命题的真假判断和应用,解题时要认真审题,仔细解答,注意公式的合理运用.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目