题目内容
若函数f(x)在x=x0处的f′(x0)=2,则| lim |
| k→0 |
| f(x0+k)-f(x0) |
| △k |
分析:根据函数导数的定义可知函数在x=x0的可导即为当自变量的增量△x=k-0,△x→0即k→0时,函数增量△f(x)=f(k+x0)-f(x0)与自变量的增量的极限存在,即得到函数f(x)在x=x0处的导数的值等于此极限的值.
解答:解:因为函数在x=x0处的f'(x0)=2,所以
=f′(x0)=2
故答案为:2
| lim |
| k→0 |
| f(x0+k)-f(x0) |
| △k |
故答案为:2
点评:此题考查学生掌握函数在某点的导数的极限定义,灵活运用转化思想解决实际问题,是一道中档题.

练习册系列答案
相关题目
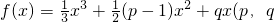 为常数).
为常数). 为常数).
为常数). 为常数).
为常数). ,则称函数f(x)在[a,b]上是下凸函数;有以下几个函数:
,则称函数f(x)在[a,b]上是下凸函数;有以下几个函数: ;
; ;
; .
.