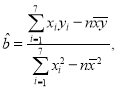题目内容
【题目】已知![]() 与函数
与函数![]() 和
和![]() 都相切,则不等式组
都相切,则不等式组![]() 所确定的平面区域在
所确定的平面区域在![]() 内的面积为( )
内的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据直线![]() 与
与![]() 和
和![]() 都相切,求得
都相切,求得![]() 的值,由此画出不等式组所表示的平面区域以及圆
的值,由此画出不等式组所表示的平面区域以及圆![]() ,由此求得正确选项.
,由此求得正确选项.
![]() .设直线
.设直线![]() 与
与![]() 相切于点
相切于点![]() ,斜率为
,斜率为![]() ,所以切线方程为
,所以切线方程为![]() ,化简得
,化简得![]() ①.令
①.令![]() ,解得
,解得![]() ,
,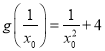 ,所以切线方程为
,所以切线方程为 ,化简得
,化简得![]() ②.由①②对比系数得
②.由①②对比系数得![]() ,化简得
,化简得![]() ③.构造函数
③.构造函数![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,所以
上递增,所以![]() 在
在![]() 处取得极小值也即是最小值,而
处取得极小值也即是最小值,而![]() ,所以
,所以![]() 有唯一解.也即方程③有唯一解
有唯一解.也即方程③有唯一解![]() .所以切线方程为
.所以切线方程为![]() .即
.即![]() .不等式组
.不等式组![]() 即
即![]() ,画出其对应的区域如下图所示.圆
,画出其对应的区域如下图所示.圆![]() 可化为
可化为![]() ,圆心为
,圆心为![]() .而方程组
.而方程组![]() 的解也是
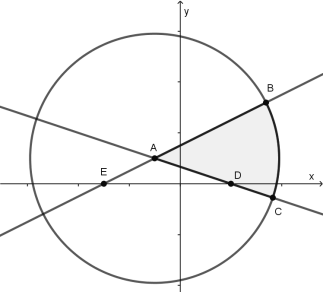
的解也是![]() .画出图像如下图所示,不等式组
.画出图像如下图所示,不等式组![]() 所确定的平面区域在
所确定的平面区域在![]() 内的部分如下图阴影部分所示.直线
内的部分如下图阴影部分所示.直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .所以
.所以![]()
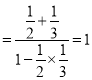 ,所以
,所以![]() ,而圆
,而圆![]() 的半径为
的半径为![]() ,所以阴影部分的面积是
,所以阴影部分的面积是![]() .
.
故选:B

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目