题目内容
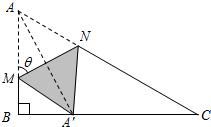 如图,直角三角形ABC中,∠B=90°,AB=1,BC=
如图,直角三角形ABC中,∠B=90°,AB=1,BC=| 3 |
(1)用θ表示线段AM的长度,并写出θ的取值范围;
(2)在△AMN中,若
| AN |
| sin∠AMN |
| MA |
| sin∠ANM |
分析:(1)设MA=MA'=x,则MB=1-x,在Rt△MBA'中,利用三角函数可求;(2)求线段A'N长度的最小值,即求线段AN长度的最小值,再利用三角恒等变换化简,从而求最值.
解答: 解:(1)设MA=MA'=x,则MB=1-x.
解:(1)设MA=MA'=x,则MB=1-x.
在Rt△MBA'中,cos(180°-2θ)=
,
∴MA=x=
=
.
∵点M在线段AB上,M点和B点不重合,A'点和B点不重合,
∴45°<θ<90°.
(2)∵∠B=90°,AB=1,BC=
,
∴∠MAN=60°,在△AMN中∠ANM=120°-θ,
=
,
AN=
=
.
令t=2sinθsin(120°-θ)=2sinθ(
sinθ+
cosθ)
=sin2θ+
sinθcosθ
=
+
sin2θ-
cos2θ=
+sin(2θ-30°).
∵45°<θ<90°,∴60°<2θ-30°<150°.
当且仅当2θ-30°=90°,θ=60°时,t有最大值
,
∴θ=60°时,A'N有最小值
.
 解:(1)设MA=MA'=x,则MB=1-x.
解:(1)设MA=MA'=x,则MB=1-x.在Rt△MBA'中,cos(180°-2θ)=
| 1-x |
| x |
∴MA=x=
| 1 |
| 1-cos2θ |
| 1 |
| 2sin2θ |
∵点M在线段AB上,M点和B点不重合,A'点和B点不重合,
∴45°<θ<90°.
(2)∵∠B=90°,AB=1,BC=
| 3 |
∴∠MAN=60°,在△AMN中∠ANM=120°-θ,
| AN |
| sinθ |
| MA |
| sin(120°-θ) |
AN=
sinθ•
| ||
| sin(120°-θ) |
| 1 |
| 2sinθsin(120°-θ) |
令t=2sinθsin(120°-θ)=2sinθ(
| 1 |
| 2 |
| ||
| 2 |
=sin2θ+
| 3 |
=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵45°<θ<90°,∴60°<2θ-30°<150°.
当且仅当2θ-30°=90°,θ=60°时,t有最大值
| 3 |
| 2 |
∴θ=60°时,A'N有最小值
| 2 |
| 3 |
点评:本题主要考查在实际问题中建立三角函数模型,从而利用三角函数中研究最值的方法解决最值问题,应注意角的范围的确定是关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 如图,直角三角形ABC中,∠B=90°,AB=1,BC=
如图,直角三角形ABC中,∠B=90°,AB=1,BC= (本题为选做题,请在下列三题中任选一题作答)
(本题为选做题,请在下列三题中任选一题作答) (2012•咸阳三模)(考生注意:请在下列三道试题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(2012•咸阳三模)(考生注意:请在下列三道试题中任选一题作答,如果多做,则按所做的第一题评阅记分)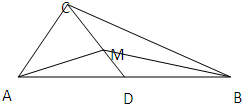 如图:直角三角形ABC中,AC⊥BC,AB=2,D是AB的中点,M是CD上的动点.
如图:直角三角形ABC中,AC⊥BC,AB=2,D是AB的中点,M是CD上的动点.