题目内容
抛物线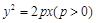 的焦点为
的焦点为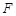 ,过焦点
,过焦点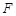 倾斜角为
倾斜角为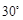 的直线交抛物线于
的直线交抛物线于 ,
,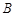 两点,点
两点,点 ,
,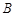 在抛物线准线上的射影分别是
在抛物线准线上的射影分别是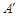 ,
,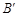 ,若四边形
,若四边形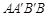 的面积为
的面积为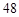 ,则抛物线的方程为____
,则抛物线的方程为____
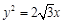
解析试题分析:抛物线的焦点为F(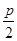 ,0),所以直线AB的方程为
,0),所以直线AB的方程为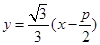 ,代入
,代入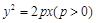 ,整理得,
,整理得,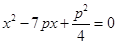 。
。
设A ,B
,B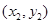 ,则由韦达定理得,
,则由韦达定理得,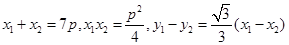 ,
,
又四边形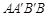 是梯形,其面积为
是梯形,其面积为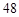 ,所以,
,所以,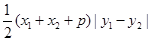 =48,
=48,
即,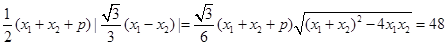 ,
,
解得,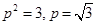 ,故答案为
,故答案为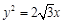 。
。
考点:本题主要考查直线方程的点斜式,抛物线的几何性质,直线与抛物线的位置关系,梯形的面积公式。
点评:中档题,本题综合性较强,对复杂式子的变形能力要求较高。涉及直线与抛物线的位置关系,应用韦达定理,实现了整体代换,简化了解题过程。

练习册系列答案
相关题目
 =1上一点P与椭圆的两个焦点F1、F2的连线互相垂直,则△PF1F2的面积为_____________
=1上一点P与椭圆的两个焦点F1、F2的连线互相垂直,则△PF1F2的面积为_____________ 轴上,渐近线方程为
轴上,渐近线方程为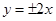 的双曲线的离心率为_______.
的双曲线的离心率为_______.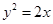 的焦点
的焦点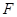 作直线
作直线 交抛物线于
交抛物线于 两点,若
两点,若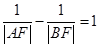 ,则直线
,则直线 。
。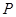 是双曲线
是双曲线 与圆
与圆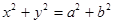 在第一象限的交点,其中
在第一象限的交点,其中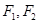 分别是双曲线的左、右焦点,若
分别是双曲线的左、右焦点,若 ,则双曲线的离心率为______________.
,则双曲线的离心率为______________.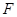 是抛物线
是抛物线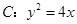 的焦点,
的焦点, 是
是 上的两个点,线段AB的中点为
上的两个点,线段AB的中点为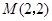 ,则
,则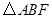 的面积等于
的面积等于 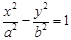 (a>0,b>0) 的左、右焦点,过F1的直线与
(a>0,b>0) 的左、右焦点,过F1的直线与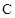 的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3 : 4 : 5,则双 曲线的离心率为 .
的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3 : 4 : 5,则双 曲线的离心率为 .
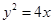 的焦点作一条倾斜角为
的焦点作一条倾斜角为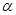 ,长度不超过8的弦,弦所在的直线与圆
,长度不超过8的弦,弦所在的直线与圆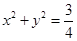
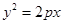 的焦点坐标为
的焦点坐标为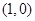 ,则
,则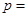 ____;准线方程为_____.
____;准线方程为_____.