题目内容
设抛物线y2=8x的准线与x轴交于点Q，若过点Q的直线l与抛物线有公共点，则直线l的斜率的取值范围是（ ）A.［
］ B.［-2，2］ C.［-1，1］ D.［-4，4］
思路分析：∵y2=8x，∴Q（-2，0）（Q为准线与x轴的交点），设过Q点的直线l方程为y= k（x+2）.
∵l与抛物线有公共点，
∴方程组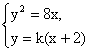有解，
即k2x2+（4k2-8）x+4k2=0有解.
∴Δ=（4k2-8）2-16k4≥0，即k2≤1.
∴-1≤k≤1.
答案：C
练习册系列答案
相关题目
设抛物线y2=8x的准线与x轴交于点Q，若过点Q的直线l与抛物线有公共点，则直线l的斜率的取值范围是（ ）
A、[-
| ||||
| B、[-2，2] | ||||
| C、[-1，1] | ||||
| D、[-4，4] |
设抛物线y2=8x的焦点为F，过F，的直线交抛物线于A（x1，y1），B（x2，y2），则y1y2=（ ）
| A、8 | B、16 | C、-8 | D、-16 |