Question

设集合A={x|x²-5x+4＞0},B={x|x²-2ax+(a+2)=0},若A∩B≠，求实数a的取值范围.

Answer 1

思路解析：本题是以集合的形式呈现，首先要能够将两个集合中的元素构成情况看清楚，然后结合条件A∩B≠，恰当地进行数形结合，从而求得实数a的取值范围.

解：∵A={x|x＜1或x＞4},

∴A∩B≠的意义是方程x²-2ax+(a+2)=0有解，且至少有一解在区间(-∞,-1)∪(4,+∞)内，但直接求解情况比较多，如果考虑“补集”，则解法较简单.

设全集U={a|Δ=(2a)²-4(a+2)≥0}={a|a≤-1或a≥2},

且P={a|关于x的方程x²-2ax+(a+2)=0的两根都在［1,4］内},

记f(x)=x²-2ax+(a+2),

∴方程f(x)=0的两根都在［1，4］内

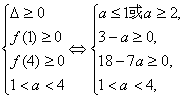
解得2≤a≤,

∴P={a|2≤a≤}.

∴所求实数a的取值范围是P={a|a≤-1或a＞}.