题目内容
已知坐标平面上的直线与x,y轴分别相交于A(3,0),B(0,3)两点,点C(cosα,sinα),其中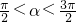 .
.
(1)若 ,求角α的值;
,求角α的值;
(2)若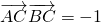 ,求sin2α的值.
,求sin2α的值.
解:(1)∵ ,
, =(cosα-3,sinα ),
=(cosα-3,sinα ), =(cosα,sinα-3),
=(cosα,sinα-3),
∴(cosα-3)2+sin2α=cos2α+(sinα-3)2.
化简可得 cosα=sinα.
又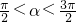 ,∴α=
,∴α= .
.
(2)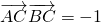 ,则 (cosα-3)cosα+sinα (sinα-3)=-1,
,则 (cosα-3)cosα+sinα (sinα-3)=-1,
化简可得 (cosα+sinα )= .
.
平方可得 1+sin2α= ,∴sin2α=-
,∴sin2α=- .
.
分析:(1)先求出 和
和 的坐标,根据
的坐标,根据 化简可得cosα=sinα,再由α的范围求出α的值.
化简可得cosα=sinα,再由α的范围求出α的值.
(2)根据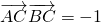 ,化简可得 (cosα+sinα )=
,化简可得 (cosα+sinα )= ,再平方可得sin2α 的值.
,再平方可得sin2α 的值.
点评:本题主要考查两个向量坐标形式的运算,求向量的模的方法,二倍角公式的应用,属于基础题.
 ,
, =(cosα-3,sinα ),
=(cosα-3,sinα ), =(cosα,sinα-3),
=(cosα,sinα-3),∴(cosα-3)2+sin2α=cos2α+(sinα-3)2.
化简可得 cosα=sinα.
又
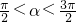 ,∴α=
,∴α= .
.(2)
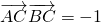 ,则 (cosα-3)cosα+sinα (sinα-3)=-1,
,则 (cosα-3)cosα+sinα (sinα-3)=-1,化简可得 (cosα+sinα )=
 .
.平方可得 1+sin2α=
 ,∴sin2α=-
,∴sin2α=- .
.分析:(1)先求出
 和
和 的坐标,根据
的坐标,根据 化简可得cosα=sinα,再由α的范围求出α的值.
化简可得cosα=sinα,再由α的范围求出α的值.(2)根据
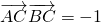 ,化简可得 (cosα+sinα )=
,化简可得 (cosα+sinα )= ,再平方可得sin2α 的值.
,再平方可得sin2α 的值.点评:本题主要考查两个向量坐标形式的运算,求向量的模的方法,二倍角公式的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
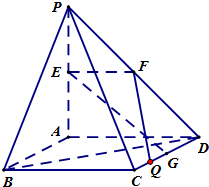 (理)如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点.
(理)如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点. 与两个定点
与两个定点 的距离之比等于5.
的距离之比等于5. 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形; ,过点
,过点 的直线
的直线 被
被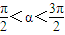 .
.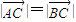 ,求角α的值;
,求角α的值; ,求sin2α的值.
,求sin2α的值.