题目内容
设数列{an}的前n项和为Sn,且满足Sn=2-an,(n=1,2,3,…)
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足b1=1,且bn+1=bn+an,求数列{bn}的通项公式;
(Ⅲ)cn=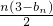 ,求cn的前n项和Tn.
,求cn的前n项和Tn.
解:(Ⅰ)由Sn=2-an①
当n=1时,S1=2-a1,∴a1=1.
取n=n+1得:Sn+1=2-an+1②
②-①得:Sn+1-Sn=an-an+1
即an+1=an-an+1,故有2an+1=an(n=1,2,3,…),
∵a1=1≠0,∴an≠0,∴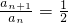 (n∈N*).
(n∈N*).
所以,数列{an}为首项a1=1,公比为 的等比数列.
的等比数列.
则an= (n∈N*).
(n∈N*).
(Ⅱ)∵bn+1=bn+an,∴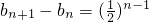 ,
,
则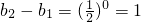 ,
,
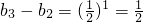 ,
,
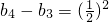 ,
,
…
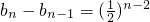 .
.
将以上n-1个等式累加得:
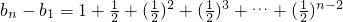
=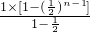
=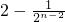 .
.
∴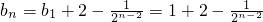 =
=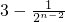 .
.
(Ⅲ)由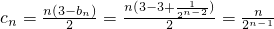 .
.
Tn=c1+c2+c3+…+cn.
得: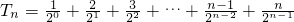 ③
③
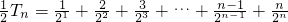 ④
④
③-④得: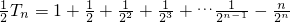
=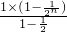
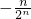
=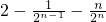 .
.
∴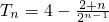 .
.
分析:(Ⅰ)在题目给出的递推式中取n=1求出a1,取n=n+1得到第二个递推式,两式作差后整理即可说明给出的数列是等比数列,则通项公式可求;
(Ⅱ)把(Ⅰ)中求出的an代入递推式bn+1=bn+an,然后利用累加法可求数列{bn}的通项公式;
(Ⅲ)把(Ⅱ)中求出的bn代入cn=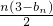 ,整理后利用错位相减法求cn的前n项和Tn.
,整理后利用错位相减法求cn的前n项和Tn.
点评:本题考查了由递推式求数列的通项公式,考查了累加法,训练了错位相减法求数列的前n项和,涉及一个等差数列和一个等比数列的积数列,错位相减是求其前n项和重要的方法.此题是中档题.
当n=1时,S1=2-a1,∴a1=1.
取n=n+1得:Sn+1=2-an+1②
②-①得:Sn+1-Sn=an-an+1
即an+1=an-an+1,故有2an+1=an(n=1,2,3,…),
∵a1=1≠0,∴an≠0,∴
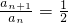 (n∈N*).
(n∈N*).所以,数列{an}为首项a1=1,公比为
 的等比数列.
的等比数列.则an=
 (n∈N*).
(n∈N*).(Ⅱ)∵bn+1=bn+an,∴
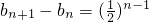 ,
,则
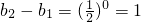 ,
,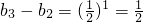 ,
,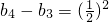 ,
,…
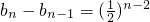 .
.将以上n-1个等式累加得:
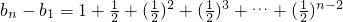
=
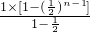
=
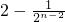 .
.∴
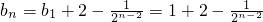 =
=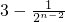 .
.(Ⅲ)由
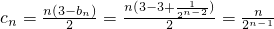 .
.Tn=c1+c2+c3+…+cn.
得:
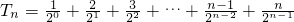 ③
③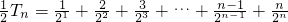 ④
④③-④得:
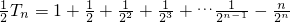
=
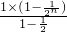
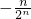
=
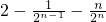 .
.∴
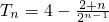 .
.分析:(Ⅰ)在题目给出的递推式中取n=1求出a1,取n=n+1得到第二个递推式,两式作差后整理即可说明给出的数列是等比数列,则通项公式可求;
(Ⅱ)把(Ⅰ)中求出的an代入递推式bn+1=bn+an,然后利用累加法可求数列{bn}的通项公式;
(Ⅲ)把(Ⅱ)中求出的bn代入cn=
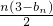 ,整理后利用错位相减法求cn的前n项和Tn.
,整理后利用错位相减法求cn的前n项和Tn.点评:本题考查了由递推式求数列的通项公式,考查了累加法,训练了错位相减法求数列的前n项和,涉及一个等差数列和一个等比数列的积数列,错位相减是求其前n项和重要的方法.此题是中档题.

练习册系列答案
相关题目