题目内容
已知函数f(x)=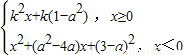 ,其中a∈R.若对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,则k的取值范围是 .
,其中a∈R.若对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,则k的取值范围是 .
【答案】分析:由于函数f(x)是分段函数,且对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,得到x=0时,f(x)=k(1-a2),进而得到,关于a的方程(3-a)2=k(1-a2)有实数解,即得△≥0,解出k即可.
解答:解:由于函数f(x)=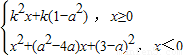 ,其中a∈R,
,其中a∈R,
则x=0时,f(x)=k(1-a2),
又由对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立
∴函数必须为连续函数,即在x=0附近的左右两侧函数值相等,
∴(3-a)2=k(1-a2)(k≠0)即(k+1)a2-6a+9-k=0有实数解,
所以△=62-4(k+1)(9-k)≥0,解得k<0或k≥8
故答案为 (-∞,0)∪[8,+∞).
点评:本题考查了二次函数的性质,通过图象比较函数值的大小,数形结合有助于我们的解题,形象直观.
解答:解:由于函数f(x)=
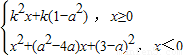 ,其中a∈R,
,其中a∈R,则x=0时,f(x)=k(1-a2),
又由对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立
∴函数必须为连续函数,即在x=0附近的左右两侧函数值相等,
∴(3-a)2=k(1-a2)(k≠0)即(k+1)a2-6a+9-k=0有实数解,
所以△=62-4(k+1)(9-k)≥0,解得k<0或k≥8
故答案为 (-∞,0)∪[8,+∞).
点评:本题考查了二次函数的性质,通过图象比较函数值的大小,数形结合有助于我们的解题,形象直观.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|