题目内容
给出如图的一个直角三角形数阵;满足每一列成等差数列,从第三行起,每一行的数成等比数列,且每一行的公比相等,如果记第一行的数为a1,第二行的第一个数为a2,第二个数为a3,第三行的第一个数为a4,…,则a83=( )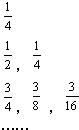
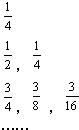
分析:若记第i行第j列的数为aij(i≥j,i,j∈N*),观察这个“直角三角形数阵”,能够发现 a11=
,ai1=a11+(i-1)×
=
,再由从第三行起,每一行的数成等比数列,可求出aij(i≥j).
| 1 |
| 4 |
| 1 |
| 4 |
| i |
| 4 |
解答: 解:先记第i行第j列的数为aij(i≥j,i,j∈N*),则:
解:先记第i行第j列的数为aij(i≥j,i,j∈N*),则:
ai1=a11+(i-1)×
=
,
aij=ai1×(
)j-1=
×(
)j-1=i×(
)j+1.
而本题中的a83位于数阵的第13行第5列,
∴a83=a(13,5)=13×(
)5+1=
故选B.
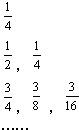 解:先记第i行第j列的数为aij(i≥j,i,j∈N*),则:
解:先记第i行第j列的数为aij(i≥j,i,j∈N*),则:ai1=a11+(i-1)×
| 1 |
| 4 |
| i |
| 4 |
aij=ai1×(
| 1 |
| 2 |
| i |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
而本题中的a83位于数阵的第13行第5列,
∴a83=a(13,5)=13×(
| 1 |
| 2 |
| 13 |
| 64 |
故选B.
点评:本题主要考查了数列的递推式,等差数列和等比数列的性质.考查了考生分析问题和解决问题的能力.

练习册系列答案
相关题目


 中,
中, 面ABC,其中正视图为
面ABC,其中正视图为
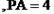 ,俯视图也为直角三角形,另一直角边长为
,俯视图也为直角三角形,另一直角边长为 。 画出侧视图并求侧视图的面积;
。 画出侧视图并求侧视图的面积;




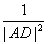 =
=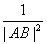 +
+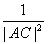 ”等,由此联想,在三棱锥O-ABC中,若三条侧棱OA,OB,OC两两互相垂直,可以推出那些结论?至少写出两个结论。(本题推出一个正确的结论并给出必要的推理证明给7分,满分不超过14分)
”等,由此联想,在三棱锥O-ABC中,若三条侧棱OA,OB,OC两两互相垂直,可以推出那些结论?至少写出两个结论。(本题推出一个正确的结论并给出必要的推理证明给7分,满分不超过14分)