题目内容
已知等差数列{an}中，公差d＞0，其前n项和为Sn，且满足a2•a3=45，a1+a4=14．
（1）求数列{an}的通项公式；
（2）设bn=2nan（n∈N+），求数列{bn}的前n项和Tn；
（3）设Fn=（4n-5）•2n+1，试比较Fn与Tn的大小．
解：（1）由已知可得
（d＞0）解得：
．
∴an=1+4（n-1）=4n-3…（4分）
（2）∵bn=2nan=（4n-3）•2n，
∴Tn=1•21+5•22+9•23+…+（4n-7）•2n-1+（4n-3）•2n，①
2Tn=1•22+5•23+…+（4n-11）•2n-1+（4n-7）•2n+（4n-3）•2n+1，②
①-②得：
-Tn=2+4（22+23+…+2n）-（4n-3）•2n+1
=2+4•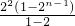
-（4n-3）•2n+1
=2+4•2n+1-16-（4n-3）•2n+1
=-（4n-7）•2n+1-14
∴Tn=（4n-7）•2n+1+14…（9分）
（3）∵Fn-Tn=（4n-5）•2n+1-（4n-7）•2n+1-14=2n+2-14，
∴当n≥2时，2n+2≥24=16＞14，即2n+1-14＞0，故Fn＞Tn；
当n=1时，2n+2=23=8＜14，即2n+1-14＜0，故Fn＜Tn．
综上所述，当n=1时，Fn＜Tn；当n≥2时，Fn＞Tn…（13分）
分析：（1）依题意可得到关于等差数列的首项与公差的方程组，解之即可；
（2）利用错位相减法即可求得数列{bn}的前n项和Tn；
（3）将Fn与Tn作差，根据结果对n分类讨论即可得到答案．
点评：本题考查等差数列的通项公式，考查数列的求和，着重考查错位相减法的应用，考查方程思想与分类讨论思想的综合应用，属于难题．
（d＞0）解得：．∴an=1+4（n-1）=4n-3…（4分）
（2）∵bn=2nan=（4n-3）•2n，
∴Tn=1•21+5•22+9•23+…+（4n-7）•2n-1+（4n-3）•2n，①
2Tn=1•22+5•23+…+（4n-11）•2n-1+（4n-7）•2n+（4n-3）•2n+1，②
①-②得：
-Tn=2+4（22+23+…+2n）-（4n-3）•2n+1
=2+4•
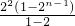-（4n-3）•2n+1=2+4•2n+1-16-（4n-3）•2n+1
=-（4n-7）•2n+1-14
∴Tn=（4n-7）•2n+1+14…（9分）
（3）∵Fn-Tn=（4n-5）•2n+1-（4n-7）•2n+1-14=2n+2-14，
∴当n≥2时，2n+2≥24=16＞14，即2n+1-14＞0，故Fn＞Tn；
当n=1时，2n+2=23=8＜14，即2n+1-14＜0，故Fn＜Tn．
综上所述，当n=1时，Fn＜Tn；当n≥2时，Fn＞Tn…（13分）
分析：（1）依题意可得到关于等差数列的首项与公差的方程组，解之即可；
（2）利用错位相减法即可求得数列{bn}的前n项和Tn；
（3）将Fn与Tn作差，根据结果对n分类讨论即可得到答案．
点评：本题考查等差数列的通项公式，考查数列的求和，着重考查错位相减法的应用，考查方程思想与分类讨论思想的综合应用，属于难题．
练习册系列答案
考前必练系列答案
相关题目
已知等差数列{an}中，a4a6=-4，a2+a8=0，n∈N*．