题目内容
设函数y=f（x）是定义在（0，+∞）上的减函数，并且满足f（xy）=f（x）+f（y），
．
（1）求f（1）的值；
（2）若存在实数m，使得f（m）=2，求m的值；
（3）如果f（x）+f（2-x）＜2，求x的取值范围．
解：（1）令x=y=1，则f（1）=f（1）+f（1），∴f（1）=0
（2）∵，
∴
∴m=
（3）∴f（x）+f（2-x）=f[x（2-x）]＜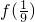
，
又由y=f（x）是定义在R+上的减函数，得：
解之得：
．
分析：（1）对于任意的x，y∈（0，+∞），f（x•y）=f（x）+f（y），令x=y=1，即可求得f（1）的值；
（2）根据题意，，令x=y=
，f（xy）=f（x）+f（y）=2；有可求得m的值；
（3）f（x）+f（2-x）=f[x（2-x）]，根据函数的单调性把函数值不等式转化为自变量不等式，解不等式即可求得结果．
点评：考查函数的单调性，及根据函数的单调性转化不等式，求抽象函数的有关命题，常采用赋值法求解，体现了转化的思想方法，属中档题．
（2）∵
，∴
∴m=
（3）∴f（x）+f（2-x）=f[x（2-x）]＜
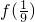，又由y=f（x）是定义在R+上的减函数，得：
解之得：．分析：（1）对于任意的x，y∈（0，+∞），f（x•y）=f（x）+f（y），令x=y=1，即可求得f（1）的值；
（2）根据题意，
，令x=y=，f（xy）=f（x）+f（y）=2；有可求得m的值；（3）f（x）+f（2-x）=f[x（2-x）]，根据函数的单调性把函数值不等式转化为自变量不等式，解不等式即可求得结果．
点评：考查函数的单调性，及根据函数的单调性转化不等式，求抽象函数的有关命题，常采用赋值法求解，体现了转化的思想方法，属中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目