题目内容
 如图,P是棱长为4的正方体ABCD-A1B1C1D1对角线AC1上一动点,若平面PBD⊥平面ABCD,则三棱锥P-ABD的体积为
如图,P是棱长为4的正方体ABCD-A1B1C1D1对角线AC1上一动点,若平面PBD⊥平面ABCD,则三棱锥P-ABD的体积为| 16 |
| 3 |
| 16 |
| 3 |
分析:利用正方体的性质、线面平行、垂直的性质、平行线分线段成比例定理、三角形中位线定理、三棱锥的体积计算公式即可得出.
解答:解:如图所示,连接AC交BD于点O,连接OP.
由正方体可得:CC1∥平面BDD1B1,∴CC1∥OP,
∵AO=OC,∴AP=PC1且OP=
CC1=2.
∵CC1⊥平面ABCD,∴PO⊥平面ABCD,即OP是三棱锥P-ABD的高.
∵S△ABD=
×4×4=8.
∴VP-ABD=
S△ABD×OP=
×8×2=
.
故答案为
.

由正方体可得:CC1∥平面BDD1B1,∴CC1∥OP,
∵AO=OC,∴AP=PC1且OP=
| 1 |
| 2 |
∵CC1⊥平面ABCD,∴PO⊥平面ABCD,即OP是三棱锥P-ABD的高.
∵S△ABD=
| 1 |
| 2 |
∴VP-ABD=
| 1 |
| 3 |
| 1 |
| 3 |
| 16 |
| 3 |
故答案为
| 16 |
| 3 |
点评:本题综合考查了正方体的性质、线面平行、垂直的性质、平行线分线段成比例定理、三角形中位线定理、三棱锥的体积计算公式,熟练掌握它们是解题的基础.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
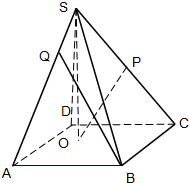 如图,已知四棱锥S-ABCD的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,SO的长为3,O到AB,AD的距离分别为2和1,P是SC的中点.
如图,已知四棱锥S-ABCD的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,SO的长为3,O到AB,AD的距离分别为2和1,P是SC的中点. 平面
平面 ,则三棱锥
,则三棱锥 的体积为 .
的体积为 .
 如图,P是棱长为4的正方体ABCD-A1B1C1D1对角线AC1上一动点,若平面PBD⊥平面ABCD,则三棱锥P-ABD的体积为________.
如图,P是棱长为4的正方体ABCD-A1B1C1D1对角线AC1上一动点,若平面PBD⊥平面ABCD,则三棱锥P-ABD的体积为________.