题目内容
设两个数列{an},{bn}满足bn=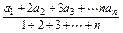 ,若{bn}为等差数列,求证:{an}也为等差数列.
,若{bn}为等差数列,求证:{an}也为等差数列.
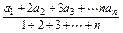 ,若{bn}为等差数列,求证:{an}也为等差数列.
,若{bn}为等差数列,求证:{an}也为等差数列.证明见解析
证明 由题意有
a1+2a2+3a3+…+nan=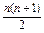 bn, ①
bn, ①
从而有a1+2a2+3a3+…+(n-1)an-1
= bn-1(n≥2), ②
bn-1(n≥2), ②
由①-②,得nan=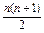 bn-
bn- bn-1,
bn-1,
整理得an=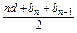 ,
,
其中d为{bn}的公差(n≥2).
从而an+1-an=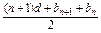 -
-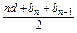
=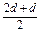 =
=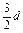 (n≥2).
(n≥2).
又a1=b1,a2=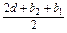
∴a2-a1=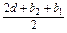 -b1=
-b1= =
= .
.
综上,an+1-an=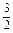 d(n∈N*).
d(n∈N*).
所以{an}是等差数列.
a1+2a2+3a3+…+nan=
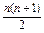 bn, ①
bn, ①从而有a1+2a2+3a3+…+(n-1)an-1
=
 bn-1(n≥2), ②
bn-1(n≥2), ②由①-②,得nan=
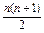 bn-
bn- bn-1,
bn-1,整理得an=
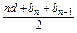 ,
,其中d为{bn}的公差(n≥2).
从而an+1-an=
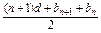 -
-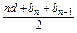
=
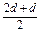 =
=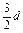 (n≥2).
(n≥2).又a1=b1,a2=
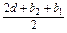
∴a2-a1=
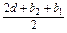 -b1=
-b1= =
= .
.综上,an+1-an=
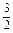 d(n∈N*).
d(n∈N*).所以{an}是等差数列.

练习册系列答案
相关题目
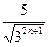 ,判断该数列是否为等差数列.
,判断该数列是否为等差数列. 是各项均为正数的等比数列,
是各项均为正数的等比数列, 是等比数列吗?为什么?
是等比数列吗?为什么? ,求Sn.
,求Sn.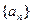 中,
中,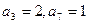 ,且数列
,且数列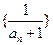 是等差数列,则
是等差数列,则 =___________.
=___________.