题目内容
在数列![]() 中,
中,![]() ,且
,且![]() 成公比不等于1的等比数列
成公比不等于1的等比数列
(1)求证:数列![]() 是等差数列; (2)求c的值;
是等差数列; (2)求c的值;
(3)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]()
⑴ 由![]() 可得
可得 即
即![]() ,
,![]() .所以数列
.所以数列![]() 为等差数列;
为等差数列;
⑵设数列![]() 的公差为
的公差为![]() ,则
,则![]() ,即
,即![]() ,
,
因为![]() 成等比数列,故
成等比数列,故![]() ,即
,即![]() ,解之可得
,解之可得![]() 或2,
或2,
因为![]() 成公比不为1的等比数列,所以
成公比不为1的等比数列,所以![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() .
.
⑶由⑵知![]() ,则
,则![]()
![]()
所以![]()
解析:
⑴对递推式![]() 进行变形可以证明数列
进行变形可以证明数列![]() 为等差数列;⑵因为
为等差数列;⑵因为![]() 成等比数列,结合⑴可求出参数c的值;⑶由前两问可以求出数列
成等比数列,结合⑴可求出参数c的值;⑶由前两问可以求出数列![]() 的通项公式,因为
的通项公式,因为![]() 从而求出
从而求出![]() .
.

练习册系列答案
相关题目
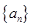 中,
中, ,且对任意
,且对任意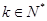 .
. ,
, ,
,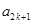 成等差数列,其公差为
成等差数列,其公差为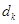 。
。 ,证明
,证明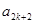 成等比数列(
成等比数列(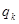 。
证明:对任意
。
证明:对任意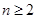 ,
, ,有
,有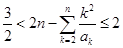
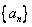 中,
中, ,且对任意
,且对任意 .
.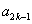 ,
,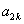 ,
, 成等差数列,其公差为
成等差数列,其公差为 。
。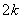 ,证明
,证明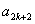 成等比数列(
成等比数列( 。
。