题目内容
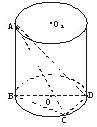 如图,AB为圆柱OO1的母线,BD为圆柱OO1下底面直径,AB=BD=2,点C为下底面圆周⊙O上的一点,CD=1.
如图,AB为圆柱OO1的母线,BD为圆柱OO1下底面直径,AB=BD=2,点C为下底面圆周⊙O上的一点,CD=1.(1)求三棱锥C-ABD的体积;
(2)求面BAD与面CAD所成二面角的大小;
(3)求BC与AD所成角的大小.
分析:(1)求三棱锥C-ABD的体积,转化为求A-BCD的体积,求出底面面积,和高即可求解.
(2)求面BAD与面CAD所成二面角的大小,先作出二面角的平面角,过B作BE⊥AD,垂足为E,过点B作BF⊥AC,垂足为点F,证明∠BEF是面ABD与面ACD所成的二面角的平面角,然后求解即可.
(3)求BC与AD所成角的大小,过点D在下底面作DG∥BC交⊙O于点G,则∠GDA为BC与AD所成的角,通过解三角形解答即可.
(2)求面BAD与面CAD所成二面角的大小,先作出二面角的平面角,过B作BE⊥AD,垂足为E,过点B作BF⊥AC,垂足为点F,证明∠BEF是面ABD与面ACD所成的二面角的平面角,然后求解即可.
(3)求BC与AD所成角的大小,过点D在下底面作DG∥BC交⊙O于点G,则∠GDA为BC与AD所成的角,通过解三角形解答即可.
解答: 解:(1)∵AB为圆柱OO1的母线,∴AB⊥下底面.
解:(1)∵AB为圆柱OO1的母线,∴AB⊥下底面.
∴AB为棱锥A-BCD的高.而点C在⊙O上,
∴△BCD为直角三角形,∠BCD=90°.
∵BD=2,CD=1,∴BC=
.
∴V三棱锥C-ABD=V三棱锥A-BCD=
×
×1×
×2=
.
(2)过B作BE⊥AD,垂足为E,过点B作BF⊥AC,垂足为点F,
连接EF.由BD为底面圆的直径,得BC⊥CD.
∵AB⊥平面BCD,BC⊥CD,
∴AC⊥CD.
而AC∩BC=C,
∴CD⊥平面ABC.
而CD?平面ADC,
∴平面ABC⊥平面ADC,且它们的交线为AC.
∵BF?平面ABC,BF⊥AC,垂足为点F,
∴BF⊥平面ACD.
而BE⊥AD,AD?平面ACD,
∴EF⊥AD.平面ABD∩平面ACD=AD,
∴∠BEF是面ABD与面ACD所成的二面角的平面角.
由BE=
AD=
,AC=
,AB=2,可求出BF=
.
∴sin∠BEF=
=
=
.
∵∠BEF为锐角,∴∠BEF=arcsin
.
故所求二面角的大小为arcsin
.
(3)过点D在下底面作DG∥BC交⊙O于点G,
则∠GDA为BC与AD所成的角.连接BG、AG,
由BD是⊙O的直径,得GD⊥BG,则AG⊥DG,BC=GD.
∴cos∠GDA=
=
=
.
∴∠GDA=arccos
.
∴所求BC与AD所成的角的大小为arccos
.
 解:(1)∵AB为圆柱OO1的母线,∴AB⊥下底面.
解:(1)∵AB为圆柱OO1的母线,∴AB⊥下底面.∴AB为棱锥A-BCD的高.而点C在⊙O上,
∴△BCD为直角三角形,∠BCD=90°.
∵BD=2,CD=1,∴BC=
| 3 |
∴V三棱锥C-ABD=V三棱锥A-BCD=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
(2)过B作BE⊥AD,垂足为E,过点B作BF⊥AC,垂足为点F,
连接EF.由BD为底面圆的直径,得BC⊥CD.
∵AB⊥平面BCD,BC⊥CD,
∴AC⊥CD.
而AC∩BC=C,
∴CD⊥平面ABC.
而CD?平面ADC,
∴平面ABC⊥平面ADC,且它们的交线为AC.
∵BF?平面ABC,BF⊥AC,垂足为点F,
∴BF⊥平面ACD.
而BE⊥AD,AD?平面ACD,
∴EF⊥AD.平面ABD∩平面ACD=AD,
∴∠BEF是面ABD与面ACD所成的二面角的平面角.
由BE=
| 1 |
| 2 |
| 2 |
| 7 |
2
| ||
| 7 |
∴sin∠BEF=
| BF |
| BE |
| ||||
|
| ||
| 7 |
∵∠BEF为锐角,∴∠BEF=arcsin
| ||
| 7 |

故所求二面角的大小为arcsin
| ||
| 7 |
(3)过点D在下底面作DG∥BC交⊙O于点G,
则∠GDA为BC与AD所成的角.连接BG、AG,
由BD是⊙O的直径,得GD⊥BG,则AG⊥DG,BC=GD.
∴cos∠GDA=
| GD |
| AD |
| ||
2
|
| ||
| 4 |
∴∠GDA=arccos
| ||
| 4 |
∴所求BC与AD所成的角的大小为arccos
| ||
| 4 |
点评:本题主要考查直线、平面的位置关系,考查圆柱的有关概念,
考查直线、平面所成角的概念及求法,考查空间想象能力和推理能力.
考查直线、平面所成角的概念及求法,考查空间想象能力和推理能力.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
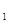 内有一个三棱柱ABC—A
内有一个三棱柱ABC—A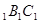 ,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。
,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。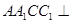 平面
平面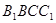 ;
; ,在圆柱OO
,在圆柱OO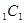
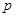 的最大值;
的最大值;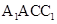 与平面
与平面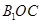 所成的角为
所成的角为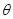
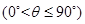 ,当
,当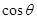 的值。
的值。