题目内容
已知点F1、F2为双曲线 (a>0,b>0)的左、右焦点,P为右支上一点,点P到右准线的距离为d,若|PF1|、|PF2|、d依次成等差数列,则此双曲线的离心率的取值范围是
(a>0,b>0)的左、右焦点,P为右支上一点,点P到右准线的距离为d,若|PF1|、|PF2|、d依次成等差数列,则此双曲线的离心率的取值范围是
- A.
 ,+∞)
,+∞) - B.(1,
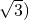
- C.(1,

- D.[2,

C
分析:根据双曲线的定义,结合等差数列的含义,得到|PF2|-|PF1|=d-|PF2|=-2a,再用圆锥曲线的统一定义,得到 ,因此d-|PF2|=d(1-e)=-2a,得到d=
,因此d-|PF2|=d(1-e)=-2a,得到d= ,最后根据双曲线右支上一点到右准线的距离的取值范围,得d≥a-
,最后根据双曲线右支上一点到右准线的距离的取值范围,得d≥a- ,建立关于a、c和e的不等式,解之即得此双曲线的离心率的取值范围.
,建立关于a、c和e的不等式,解之即得此双曲线的离心率的取值范围.
解答:∵|PF1|、|PF2|、d依次成等差数列,
∴|PF2|-|PF1|=d-|PF2|,
∵P为双曲线 右支上一点,(a>0,b>0)
右支上一点,(a>0,b>0)
∴|PF2|-|PF1|=-2a=d-|PF2|,
设双曲线的离心率是e,根据圆锥曲线的统一定义,
得到 ,所以d-|PF2|=d(1-e)=-2a
,所以d-|PF2|=d(1-e)=-2a
∴根据双曲线右支上一点到右准线的距离的取值范围,得:d= ≥a-
≥a- ,
,
上式的两边都除以a,得: ≥1-
≥1- ,解此不等式得:
,解此不等式得: ≤e≤
≤e≤
又∵双曲线的离心率e>1,
∴e∈
故选C
点评:本题以等差数列为载体,求双曲线的离心率,着重考查了双曲线的简单性质和等差数列的概念等知识点,属于中档题.
分析:根据双曲线的定义,结合等差数列的含义,得到|PF2|-|PF1|=d-|PF2|=-2a,再用圆锥曲线的统一定义,得到
 ,因此d-|PF2|=d(1-e)=-2a,得到d=
,因此d-|PF2|=d(1-e)=-2a,得到d= ,最后根据双曲线右支上一点到右准线的距离的取值范围,得d≥a-
,最后根据双曲线右支上一点到右准线的距离的取值范围,得d≥a- ,建立关于a、c和e的不等式,解之即得此双曲线的离心率的取值范围.
,建立关于a、c和e的不等式,解之即得此双曲线的离心率的取值范围.解答:∵|PF1|、|PF2|、d依次成等差数列,
∴|PF2|-|PF1|=d-|PF2|,
∵P为双曲线
 右支上一点,(a>0,b>0)
右支上一点,(a>0,b>0)∴|PF2|-|PF1|=-2a=d-|PF2|,
设双曲线的离心率是e,根据圆锥曲线的统一定义,
得到
 ,所以d-|PF2|=d(1-e)=-2a
,所以d-|PF2|=d(1-e)=-2a∴根据双曲线右支上一点到右准线的距离的取值范围,得:d=
 ≥a-
≥a- ,
,上式的两边都除以a,得:
 ≥1-
≥1- ,解此不等式得:
,解此不等式得: ≤e≤
≤e≤
又∵双曲线的离心率e>1,
∴e∈

故选C
点评:本题以等差数列为载体,求双曲线的离心率,着重考查了双曲线的简单性质和等差数列的概念等知识点,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目