Question

直三棱柱ABC-A₁B₁C₁中，AB=5，AC=4，BC=3，AA₁=4，D是AB的中点．

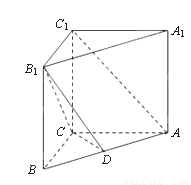
（1）求证：AC⊥B₁C；

（2）求证：AC₁∥平面B₁CD；

 

Answer 1

【答案】

（Ⅰ）证明见解析（Ⅱ）证明见解析.

【解析】

试题分析：（Ⅰ）要证明“线线垂直”，可通过证明“线面垂直”而得到.

由于在△ABC中，AB=5，AC=4，BC=3，

所以  AC⊥BC．又在直三棱柱ABC-A₁B₁C₁中C C₁⊥AC．

因此可得到AC⊥平面B B₁C₁C．证得AC⊥B₁C．

（Ⅱ）证明“线线平行”，往往可通过证明“线线平行”或“面面平行”而得到.

注意连结BC₁，利用DE为△ABC₁的中位线，得到 DE// AC₁．

从而可得AC₁∥平面B₁CD．

立体几何中的证明问题，要注意表达的规范性及层次性.

试题解析：证明：（Ⅰ）在△ABC中，因为AB=5，AC=4，BC=3，

所以AC⊥BC．

因为直三棱柱ABC-A₁B₁C₁，所以CC₁⊥AC．

因为BC∩AC=C，所以AC⊥平面BB₁C₁C．

所以AC⊥B₁C．

（Ⅱ）连结BC₁，交B₁C于E．

因为直三棱柱ABC-A₁B₁C₁，

所以侧面BB₁C₁C为矩形，且E为B₁C中点.

又D是AB中点，所以DE为△ABC₁的中位线，所以DE//AC₁．

因为DE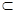平面B₁CD，AC₁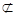平面B₁CD，

所以AC₁∥平面B₁CD．

考点：垂直关系，平行关系.