题目内容
如图所示，四棱锥P—ABCD的底面ABCD是半径为R的圆的内接四边形，其中BD是圆的直径
。
（1）求线段PD的长；
（2）若
，求三棱锥P—ABC的体积。
 |
解：（1）因为BD是圆的直径，
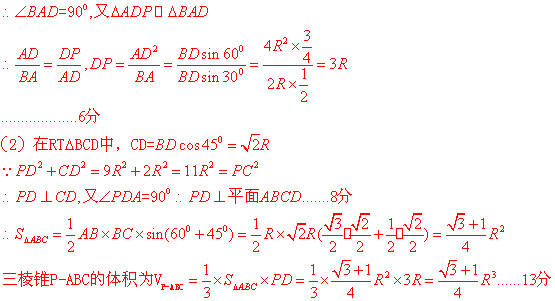
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
新思维假期作业暑假吉林大学出版社系列答案蓝天教育暑假优化学习系列答案题目内容
如图所示，四棱锥P—ABCD的底面ABCD是半径为R的圆的内接四边形，其中BD是圆的直径。
（1）求线段PD的长；
（2）若，求三棱锥P—ABC的体积。
|
解：（1）因为BD是圆的直径，
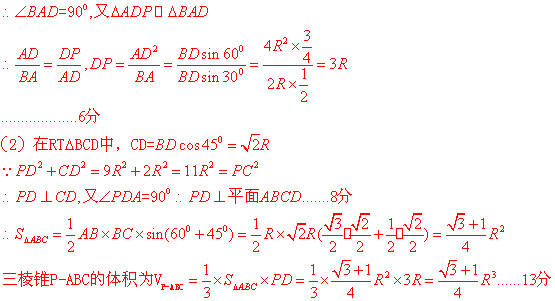
新思维假期作业暑假吉林大学出版社系列答案蓝天教育暑假优化学习系列答案
如图所示，四棱锥P-ABCD的底面为直角梯形，∠ADC=∠DCB=90°，AD=1，BC=3，PC=CD=2，PC⊥底面ABCD，E为AB的中点．
如图所示，四棱锥P-ABCD的底面是一个矩形，AB=3．AD=1．又PA⊥AB，PA=4，
如图所示，四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形，其中BD是圆的直径，∠ABD=60°，∠BDC=45°，△ADP～△BAD．
（2012•烟台一模）如图所示，四棱锥P-ABCD中，ABCD为正方形，PA⊥AD，E，F，G分别是线段PA，PD，CD的中点．
如图所示，四棱锥P-ABCD底面是直角梯形，BA⊥AD，CD⊥AD，CD=2AB，PA⊥底面ABCD，E为PC的中点，PA=AD=AB=1．