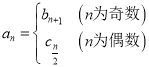题目内容
【题目】已知定义在![]() 上的函数
上的函数![]() 和数列
和数列![]() 满足下列条件:
满足下列条件:![]() ,当
,当![]() 且
且![]() 时,
时,![]() 且
且![]() ,其中
,其中![]() 均为非零常数.
均为非零常数.
(1)数列![]() 是等差数列,求
是等差数列,求![]() 的值;
的值;
(2)令![]() ,若
,若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)证明:![]() 数列是等比数列的充要条件是
数列是等比数列的充要条件是![]() .
.
【答案】(1)1(2)![]()
![]() (3)证明见解析
(3)证明见解析
【解析】
(1)由题意知![]() ,
,![]()
![]() ,得
,得![]() ,再由等差数列,即可求解
,再由等差数列,即可求解![]() 值;
值;
(2)由![]() ,可得
,可得![]() ,因此
,因此![]() ,由此可知,数列
,由此可知,数列![]() 是一个公比为
是一个公比为![]() 的等比数列.
的等比数列.
(3)先进行充分性证明:若![]() 则
则![]() 数列是等比数列;再进行必要性证明:若
数列是等比数列;再进行必要性证明:若![]() 数列是等比数列,则
数列是等比数列,则![]() .
.
(1)由已知![]() ,
,![]() ,
,
得![]() ,
,
由数列![]() 是等差数列,得
是等差数列,得![]() ,
,
所以,![]() ,
,![]() ,
,
得![]() .
.
(2)由![]() ,可得
,可得![]() ,
,
且当![]() 时,
时,
![]()
![]() ,
,
所以,当![]() 时,
时,![]() ,
,
因此,数列![]() 是一个公比为
是一个公比为![]() 的等比数列.
的等比数列.
故通项公式为![]()
(3)![]() 是等比数列的充要条件是
是等比数列的充要条件是![]() ,
,
充分性证明:若![]() ,则由已知
,则由已知![]() ,
,![]()
得![]() ,所以,
,所以,![]() 是等比数列.
是等比数列.
必要性证明:若![]() 是等比数列,由(2)知,
是等比数列,由(2)知,![]() ,
,
![]()
![]() ,
,
![]() .
.
当![]() 时,
时,![]() .上式对
.上式对![]() 也成立,
也成立,
所以,数列![]() 的通项公式为:
的通项公式为:![]() .
.
所以,当![]() 时,数列
时,数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列.
为公差的等差数列.
所以,![]() .
.
当![]() 时,
时,![]() .上式对
.上式对![]() 也成立,
也成立,
所以,![]()
![]() .
.
所以,![]() .
.
即,等式![]() 对于任意实数
对于任意实数![]() 均成立.
均成立.
所以![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】自2009年以来,菜鸟网络物流和淘宝商城双十一活动已经走过十年,某数学兴趣小组收集了近五年双十一当天菜鸟网络物流订单数据如下表.并且查知这五年订单数的平均数约为6.5亿件.
年份代码 | 1 | 2 | 3 | 4 | 5 |
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
订单数 | 2.8 | 4.7 |
| 8.1 | 10.4 |
(1)现发现表中一个数据![]() 看不清,试求出表中
看不清,试求出表中![]() 的值,并根据收集的这些数据和下列有关参考数据说明函数
的值,并根据收集的这些数据和下列有关参考数据说明函数![]() ,
,![]() 中,哪一个类型更适合
中,哪一个类型更适合![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)依据你的判断,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)预测菜鸟网络物流2019年的订单数.
参考数据:
订单数 | 2.8 | 4.7 |
| 8.1 | 10.4 |
| 1.03 | 1.55 | 1.87 | 2.09 | 2.34 |
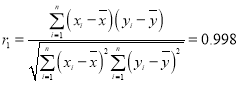 ,
,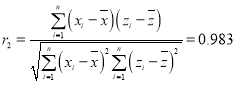 .
.
参考公式: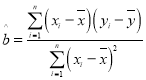 ,
,![]() .
.