题目内容
已知函数f(x)=lnx,g(x)=x2-1.(1)求函数h(x)=f(x)-
 g(x)的最值;
g(x)的最值;(2)对于一切正数x,恒有f(x)≤k(x2-1)成立,求实数k的取值组成的集合.
【答案】分析:(1)求导函数,确定函数的单调性,从而可求函数h(x)最大值;
(2)构造函数F(x)=lnx-k(x2-1),对于一切正数x,恒有f(x)≤k(x2-1)成立,等价于F(x)≤0恒成立.求导函数,再进行分类讨论,即可确定实数k的取值组成的集合.
解答:解:(1)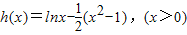
求导函数可得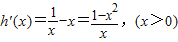 ,所以函数h(x)在(0,1)递增,在(1,+∞)递减.
,所以函数h(x)在(0,1)递增,在(1,+∞)递减.
所以h(x)的最大值为h(1)=0.….(3分)
(2)令函数F(x)=lnx-k(x2-1)得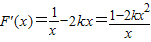
当k≤0时,F′(x)>0恒成立,所以F(x)在(0,+∞)递增,
故x>1时,F(x)>F(0)=0不满足题意.….(5分)
当k>0时,当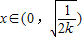 时,F′(x)>0恒成立,函数F(x)递增;
时,F′(x)>0恒成立,函数F(x)递增;
当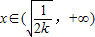 时,F′(x)<0恒成立,函数F(x)递减.
时,F′(x)<0恒成立,函数F(x)递减.
所以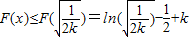 ;即 F(x)的最大值
;即 F(x)的最大值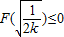 ….(8分)
….(8分)
令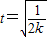 ,则
,则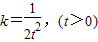 .
.
令函数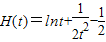 ,
,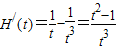
所以当t∈(0,1)时,函数H(t)递减;当t∈(1,+∞)时,函数H(x)递增;
所以函数H(t)≥H(1)=0,
从而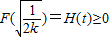 ,∴
,∴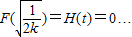 (11分)
(11分)
就必须当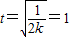 ,即
,即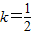 时成立.
时成立.
综上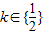 .….(12分)
.….(12分)
点评:本题考查导数知识的运用,考查构造函数法解决不等式恒成立问题,解题的关键是构造函数,确定函数的最值.
(2)构造函数F(x)=lnx-k(x2-1),对于一切正数x,恒有f(x)≤k(x2-1)成立,等价于F(x)≤0恒成立.求导函数,再进行分类讨论,即可确定实数k的取值组成的集合.
解答:解:(1)
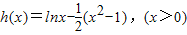
求导函数可得
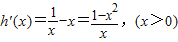 ,所以函数h(x)在(0,1)递增,在(1,+∞)递减.
,所以函数h(x)在(0,1)递增,在(1,+∞)递减.所以h(x)的最大值为h(1)=0.….(3分)
(2)令函数F(x)=lnx-k(x2-1)得
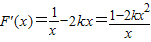
当k≤0时,F′(x)>0恒成立,所以F(x)在(0,+∞)递增,
故x>1时,F(x)>F(0)=0不满足题意.….(5分)
当k>0时,当
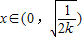 时,F′(x)>0恒成立,函数F(x)递增;
时,F′(x)>0恒成立,函数F(x)递增;当
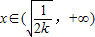 时,F′(x)<0恒成立,函数F(x)递减.
时,F′(x)<0恒成立,函数F(x)递减.所以
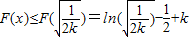 ;即 F(x)的最大值
;即 F(x)的最大值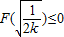 ….(8分)
….(8分)令
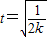 ,则
,则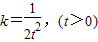 .
.令函数
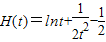 ,
,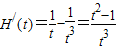
所以当t∈(0,1)时,函数H(t)递减;当t∈(1,+∞)时,函数H(x)递增;
所以函数H(t)≥H(1)=0,
从而
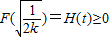 ,∴
,∴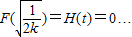 (11分)
(11分)就必须当
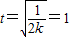 ,即
,即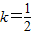 时成立.
时成立.综上
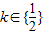 .….(12分)
.….(12分)点评:本题考查导数知识的运用,考查构造函数法解决不等式恒成立问题,解题的关键是构造函数,确定函数的最值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目