Question

根据下面的要求，求

1

1×2

+

1

2×3

+

1

3×4

+…+

1

99×100

的值的程序框图．
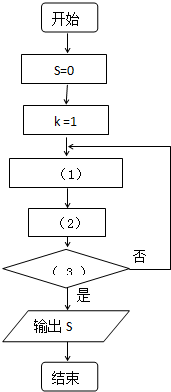
标号（1）处填

S=S+

1

k(K+1)

．
标号（2）处填

k=k-1

．
标号（3）处填

i≥99

．

Answer 1

分析：分析程序的功能结合已知的流程图，易得本题循环体中的两条语句功能分别为累加和改变循环变量的值，及循环的终值，我们知道循环共进行了99次，其步长为1，又由S每次累加的量是 p，故应该先改变循环变量的值，再进行累加．从而得出答案．

解答：解：∵循环变量的初值为1，终值为99，
根据循环要实现的功能，
故循环体内的（1）语句应为：S=S+

1

k(K+1)

；
（2）语句应为：k=k-1；
（3）语句应为：i≥99．
故答案为：（1）S=S+

1

k(K+1)

；（2）k=k-1；（3）i≥99．

点评：本题考查的知识点是利用循环结构进行累加（乘）运算，其中根据循环变得初值、终值、循环体执行的次数，确定步长及累加量的表达式，及改变循环变量的值的语句与累加语句的次序是解答本题的关键．