题目内容
12.设函数f(x)=ln(1+x),g(x)=xf′(x),其中f′(x)是f(x)的导函数.(1)求f(x)在x=0处的切线方程;
(2)若f(x)≥ag(x)(x≥0)恒成立,求实数a的取值范围;
(3)设n∈N+,比较g(1)+g(2)+…+g(n)与n-f(n)的大小,并加以证明.
分析 (1)求导数,可得切线的斜率,即可得f(x)在x=0处的切线方程;
(2)由已知得到ln(1+x)≥$\frac{ax}{1+x}$恒成立,构造函数φ(x)=ln(1+x)-$\frac{ax}{1+x}$(x≥0),利用导数求出函数的最小值即可;
(3)在(2)中取a=1,可得ln(1+x)>$\frac{x}{1+x}$,x>0,令x=$\frac{1}{n}$,则ln$\frac{n+1}{n}$>$\frac{1}{n+1}$,n依次取1,2,3…,然后各式相加即得到不等式.
解答 解:(1)f(x)=ln(1+x),则f′(x)=$\frac{1}{1+x}$,
x=0时,f(0)=0,f′(0)=1,
∴f(x)在x=0处的切线方程为y=x;
(2)已知f(x)≥ag(x)恒成立,即ln(1+x)≥$\frac{ax}{1+x}$恒成立.
设φ(x)=ln(1+x)-$\frac{ax}{1+x}$(x≥0),则φ′(x)=$\frac{x+1-a}{(1+x)^{2}}$,
当a≤1时,φ′(x)≥0(仅当x=0,a=1时取等号成立),
∴φ(x)在[0,+∞)上单调递增,
又φ(0)=0,
∴φ(x)≥0在[0,+∞)上恒成立.
∴当a≤1时,ln(1+x)≥$\frac{ax}{1+x}$恒成立,(仅当x=0时等号成立)
当a>1时,对x∈(0,a-1]有φ′(x)<0,∴φ(x)在∈(0,a-1]上单调递减,
∴φ(a-1)<φ(0)=0,即当a>1时存在x>0使φ(x)<0,
故知ln(1+x)≥$\frac{ax}{1+x}$不恒成立,
综上可知,实数a的取值范围是(-∞,1].
(3)由题设知,g(1)+g(2)+…+g(n)=$\frac{1}{2}$+$\frac{2}{3}$+…+$\frac{n}{n+1}$,
n-f(n)=n-ln(n+1),
比较结果为g(1)+g(2)+…+g(n)>n-ln(n+1)
证明如下:上述不等式等价于$\frac{1}{2}$+$\frac{2}{3}$+…+$\frac{n}{n+1}$<ln(n+1),
在(Ⅱ)中取a=1,可得ln(1+x)>$\frac{x}{1+x}$,x>0,
令x=$\frac{1}{n}$,则ln$\frac{n+1}{n}$>$\frac{1}{n+1}$,
故有ln2-ln1>$\frac{1}{2}$,
ln3-ln2>$\frac{1}{3}$,
…
ln(n+1)-lnn>$\frac{1}{n+1}$,
上述各式相加可得ln(n+1)>$\frac{1}{2}$+$\frac{2}{3}$+…+$\frac{n}{n+1}$,结论得证.
点评 本题考查数学归纳法;考查构造函数解决不等式问题;考查利用导数求函数的最值,证明不等式,属于一道综合题.

| A. | $\frac{3}{2}$ | B. | 2 | C. | 3 | D. | $\frac{5}{2}$ |
| A. | {$\sqrt{2}$} | B. | {2} | C. | {-$\sqrt{2}$,1,$\sqrt{2}$,2} | D. | {-2,1,$\sqrt{2}$,2} |
| A. | 3$\root{3}{9}$ | B. | 1+2$\sqrt{2}$ | C. | 7 | D. | 6 |
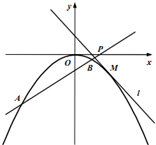 已知曲线C:x2=-2py(p>0),点M是曲线C上的一个动点,过点M且与曲线C相切的直线l的方程为x+y-1=0.
已知曲线C:x2=-2py(p>0),点M是曲线C上的一个动点,过点M且与曲线C相切的直线l的方程为x+y-1=0.
 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M、N分别是这段图象的最高点和最低点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0(O为坐标原点),则A=$\frac{\sqrt{7}}{12}$π.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M、N分别是这段图象的最高点和最低点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0(O为坐标原点),则A=$\frac{\sqrt{7}}{12}$π.