题目内容
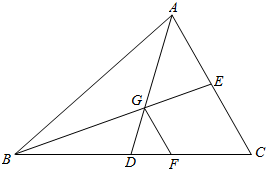
14.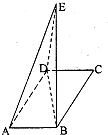 如图,在平行四边形么BCD中,∠DAB=60°,AD=4,AB=2,将△CBD沿BD折起到△EBD的位置.
如图,在平行四边形么BCD中,∠DAB=60°,AD=4,AB=2,将△CBD沿BD折起到△EBD的位置.(Ⅰ)求证:BD⊥平面CDE;
(Ⅱ)当∠CDE取何值时,三棱锥E-ABD的体积取最大值?并求此时三棱锥E-ABD的侧面积.
分析 (Ⅰ)证明:AB⊥DE,可得BD⊥CD,BD⊥DE,即可证明BD⊥平面CDE;
(Ⅱ)当∠CDE=90°时,h=ED=2,三棱锥E-ABD的体积取最大值,再求此时三棱E-ABD的侧面积.
解答 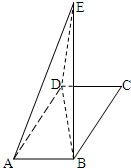 (I)证明:在△ABD中,∵∠DAB=60°,AB=2,AD=4,
(I)证明:在△ABD中,∵∠DAB=60°,AB=2,AD=4,
∴BD=$\sqrt{4+16-2×2×4×\frac{1}{2}}$=2$\sqrt{3}$,
∴AB2+BD2=AD2,
∴AB⊥DE
∵AB∥CD,
∴BD⊥CD,BD⊥DE,
又∵CD∩DE=D,∴BD⊥平面CDE …(6分)
(Ⅱ)解:设E点到平面ABCD距离为h,则h≤ED=2.
由(I)知BD⊥DE
当DE⊥CD时,
∵BD∩CD=D,∴ED⊥平面ABCD,
∴当∠CDE=90°时,h=ED=2,三棱锥E-ABD的体积取最大值.
此时ED⊥平面ABCD,∴ED⊥AD、ED⊥BD
在Rt△DBE中,∵DB=2$\sqrt{3}$,DE=DC=AB=2,
∴S△BDE=$\frac{1}{2}$DB•DE=2$\sqrt{3}$,
在Rt△ADE中,S△ADE=$\frac{1}{2}$AD•DE=4,
∵AB⊥BD,BD⊥DE,BD∩DE=D,∴AB⊥平面BDE,∴AB⊥BE.
∵BE=BC=AD=4,
∴S△ABE=$\frac{1}{2}$AB•BE=4,
综上,∠CDE=90°时,三棱锥E-ABD体积取最大值,此时侧面积S=8+2$\sqrt{3}$.…(12分)
点评 本题考查棱锥的侧面积,直线和平面的垂直的证明,考查学生分析解决问题的能力,是中档题.

练习册系列答案
相关题目
2.已知函数f(x)=$\sqrt{{x}^{2}-2x-3}$的定义域为F,g(x)=$\sqrt{\frac{x+1}{x-3}}$的定义域为G,那么集合F,G的关系是( )
| A. | F=G | B. | F⊆G | C. | G⊆F | D. | F∪G=G |
9.一个几何体的三视图如图所示,其中俯视图与侧视图都是半径为2的圆,则这个几何体的体积是( )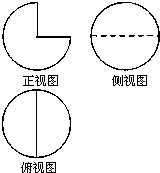

| A. | 8π | B. | 16π | C. | $\frac{8π}{3}$ | D. | $\frac{16π}{3}$ |
19.某几何体的三视图如图所示,图中方格的长度为1,则该几何体的外接球的体积为( )
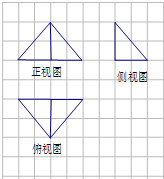

| A. | $\frac{8}{3}π$ | B. | 8π | C. | $\frac{32}{3}π$ | D. | $\frac{16}{3}π$ |