题目内容
已知中心在原点的双曲线C的右焦点为(2,0),右顶点为((1)求双曲线C的方程;
(2)若直线l:y=kx+2与双曲线C恒有两个不同的交点A和B,且![]() ·
·![]() >2(其中O为原点),求k的取值范围.
>2(其中O为原点),求k的取值范围.
思路分析:由C与l恒有两个不同的交点,求出k2<0且k2≠![]() ,再由
,再由![]() ·
·![]() >2,即可求得最后k的范围.
>2,即可求得最后k的范围.
解:(1)设双曲线方程为
![]() -
-![]() =1(a>0,b>0).
=1(a>0,b>0).
由已知得a=![]() ,c=2,再由a2+b2=22,得b2=1.
,c=2,再由a2+b2=22,得b2=1.
故双曲线C的方程为![]() -y2=1.
-y2=1.
(2)将y=kx+![]() 代入
代入![]() -y2=1,得
-y2=1,得
(1-3k2)x2-6![]() kx-9=0.
kx-9=0.
由直线l与双曲线交于不同的两点得
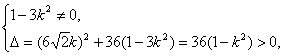
即k2≠![]() 且k2<1. ①
且k2<1. ①
设A(xA,yB),B(xB,yB),则
xA+xB=![]() ,xAxB=
,xAxB=![]() ,
,
由![]() ·
·![]() >2,得xAxB+yAyB>2,而
>2,得xAxB+yAyB>2,而
xAxB+yAyB=xAxB+(kxA+2)(kxB+2)
=(k2+1)xAxB+2k(xA+xB)+2
=(k2+1)![]() +2k
+2k![]() +2
+2
=![]() .
.
于是![]() >2,即
>2,即![]() >0.
>0.
解此不等式得![]() <k2<3. ②
<k2<3. ②
由①②得![]() <k2<1,故k的取值范围是(-1,-
<k2<1,故k的取值范围是(-1,-![]() )∪(
)∪(![]() ,1).
,1).

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目