题目内容
设函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,-π<φ<π)在 处取得最大值2,其图象与x轴的相邻两个交点的距离为
处取得最大值2,其图象与x轴的相邻两个交点的距离为
( I)求f(x)的解析式;
( II)求函数g(x)=f(-x)的单调递减区间.
解:(I)由题意,T=π,∴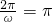 ,∴ω=2
,∴ω=2
∵函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,-π<φ<π)在 处取得最大值2,
处取得最大值2,
∴A=2,sin(2× +φ)=1,∴φ=
+φ)=1,∴φ=
∴f(x)的解析式为f(x)=2sin(2x+ );
);
(II)函数g(x)=f(-x)=2sin(-2x+ );
);
令- ≤-2x+
≤-2x+ ≤
≤ (k∈Z)
(k∈Z)
∴ (k∈Z)
(k∈Z)
∴函数的单调递减区间为 (k∈Z)
(k∈Z)
分析:(I)先确定函数的周期,可得ω的值,利用函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,-π<φ<π)在 处取得最大值2,即可求得f(x)的解析式;
处取得最大值2,即可求得f(x)的解析式;
(II)函数g(x)=f(-x)=2sin(-2x+ ),利用正弦函数的单调增区间,可得函数的单调递减区间.
),利用正弦函数的单调增区间,可得函数的单调递减区间.
点评:本题考查函数的解析式,考查函数的单调性,正确求函数的解析式是关键.
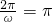 ,∴ω=2
,∴ω=2∵函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,-π<φ<π)在
 处取得最大值2,
处取得最大值2,∴A=2,sin(2×
 +φ)=1,∴φ=
+φ)=1,∴φ=
∴f(x)的解析式为f(x)=2sin(2x+
 );
);(II)函数g(x)=f(-x)=2sin(-2x+
 );
);令-
 ≤-2x+
≤-2x+ ≤
≤ (k∈Z)
(k∈Z)∴
 (k∈Z)
(k∈Z)∴函数的单调递减区间为
 (k∈Z)
(k∈Z)分析:(I)先确定函数的周期,可得ω的值,利用函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,-π<φ<π)在
 处取得最大值2,即可求得f(x)的解析式;
处取得最大值2,即可求得f(x)的解析式;(II)函数g(x)=f(-x)=2sin(-2x+
 ),利用正弦函数的单调增区间,可得函数的单调递减区间.
),利用正弦函数的单调增区间,可得函数的单调递减区间.点评:本题考查函数的解析式,考查函数的单调性,正确求函数的解析式是关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 (n∈N*)
(n∈N*) .
. 对不小于2的正整数恒成立,求x的取值范围.
对不小于2的正整数恒成立,求x的取值范围.