题目内容
某厂生产甲、乙两种产品,甲种产品每单位需A种原料8克,B种原料24克,每单位利润60元;乙种产品每单位需A种原料和B种原料各16克,每单位利润80元。现有A种原料2400克,B种原料2880克,问甲、乙两产品各生产多少单位,工厂可获得最大利润(原料不再外购,产品可完全售出)。
解:设生产甲、乙两种产品分别为x单位、y单位,所获利润为z元,
则z=60x+80y,
依题意,有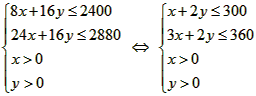 ,
,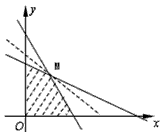
作出不等式组表示的平面区域如图
由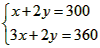 得M(30,135) ,
得M(30,135) ,
将直线60x+80=z平移过点M,即x=30,y=135时,z取到最大值,
∴甲、乙两种产品分别生产30单位和135单位时,工厂可获得最大利润。
则z=60x+80y,
依题意,有
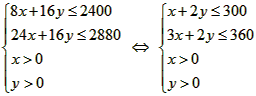 ,
,
作出不等式组表示的平面区域如图
由
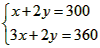 得M(30,135) ,
得M(30,135) , 将直线60x+80=z平移过点M,即x=30,y=135时,z取到最大值,
∴甲、乙两种产品分别生产30单位和135单位时,工厂可获得最大利润。

练习册系列答案
相关题目