题目内容
已知椭圆是以二次函数y=-
x2+2的图象与x轴的交点为焦点,以该函数图象的顶点为椭圆的一个顶点.
(1)求椭圆的标准方程;
(2)椭圆上位于第一象限内的一点P的横坐标为
,,求△PF1F2面积.(F1、F2分别椭圆的两个焦点).
| 1 |
| 8 |
(1)求椭圆的标准方程;
(2)椭圆上位于第一象限内的一点P的横坐标为
| 15 |
(1)由已知:椭圆的焦点在x轴上,
可设为
+
=1(a>b>0)
由-
x2+2=0可得:x=±4
又∵函数y=x2+2=0的顶点为(0,2)
∴c=4,b=2,∴a2=20
∴椭圆方程为
+
=1
(2)由xP=
代入(1)中的方程可得:yP=1(yP>0)
又∵|F1F2|=2c=8
∴S△PF1F2=
•|F1F2|•yP=
×8×1=4.
可设为
| x2 |
| a2 |
| y2 |
| b2 |
由-
| 1 |
| 8 |
又∵函数y=x2+2=0的顶点为(0,2)
∴c=4,b=2,∴a2=20
∴椭圆方程为
| x2 |
| 20 |
| y2 |
| 4 |
(2)由xP=
| 15 |
又∵|F1F2|=2c=8
∴S△PF1F2=
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
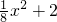 的图象与x轴的交点为焦点,以该函数图象的顶点为椭圆的一个顶点.
的图象与x轴的交点为焦点,以该函数图象的顶点为椭圆的一个顶点. ,,求△PF1F2面积.(F1、F2分别椭圆的两个焦点).
,,求△PF1F2面积.(F1、F2分别椭圆的两个焦点).