题目内容
5位员工甲、乙、丙、丁、戊参加单位的技能测试,已知他们测试合格的概率分别是| 3 |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
(Ⅰ)求他们中恰好有一人通过测试的概率;
(Ⅱ)求他们中恰好有两人通过测试且甲、乙两人不都通过测试的概率.
分析:(I)根据所给的概率不同,甲、乙通过测试分别为A、B,丙、丁、戊三人通过测试是独立重复试验,三人中有k人通过测试的概率,根据独立重复试验和互斥事件的概率得到结果.
(II)恰好有两人通过测试且甲、乙两人不都通过包括三种情况,这三种情况之间是互斥关系,根据独立重复试验和互斥事件的概率公式得到结果.
(II)恰好有两人通过测试且甲、乙两人不都通过包括三种情况,这三种情况之间是互斥关系,根据独立重复试验和互斥事件的概率公式得到结果.
解答:解:(Ⅰ)记甲、乙通过测试分别为A、B,丙、丁、戊三人通过测试是独立重复试验,三人中有k人通过测试的概率为P3(k)=
(
)k(
)3-k,k=0,1,2,3.
他们中恰有一人通过测试的概率为P(
•B+A•
)•P3(0)+P(
•
)•P3(1)=(
•
+
•
)(
)3+(
•
)
•
•(
)2=
.
答:他们中恰有一人通过测试的概率为
.
(Ⅱ)他们中恰好有两人通过测试且甲、乙两人不都通过测试的概率为
P(
?B+A?
)?P3(1)+P(
?
)?P3(2)=(
?
+
?
)C
?
?(
)2+(
?
)C(
)2?
=
.
答:他们中恰好有两人通过测试且甲、乙两人不都通过测试的概率为
.
| C | k 3 |
| 2 |
| 3 |
| 1 |
| 3 |
他们中恰有一人通过测试的概率为P(
. |
| A |
. |
| B |
. |
| A |
. |
| B |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| C | 1 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 5 |
| 108 |
答:他们中恰有一人通过测试的概率为
| 5 |
| 108 |
(Ⅱ)他们中恰好有两人通过测试且甲、乙两人不都通过测试的概率为
P(
. |
| A |
. |
| B |
. |
| A |
. |
| B |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 6 |
答:他们中恰好有两人通过测试且甲、乙两人不都通过测试的概率为
| 1 |
| 6 |
点评:考查相互独立事件的概率与独立重复试验的概率.本题完全可以只看作是相互独立事件的概率问题,考虑到丙、丁、戊三人测试合格的概率相同,可以看作是独立重复试验,简化了运算.本题要求学生对独立重复试验有良好的理解.

练习册系列答案
相关题目
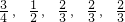 .
. .
. .
.