题目内容
已知复数z1=bcosC+(a+c)i,z2=(2a-c)cosB+4i,且z1=z2,其中A、B、C为△ABC的内角,a、b、c为角A、B、C所对的边.(Ⅰ)求角B的大小;
(Ⅱ)若
 ,求△ABC的面积.
,求△ABC的面积.
【答案】分析:(Ⅰ)利用复数相等的条件得到关于cosB的解析式,再由正弦定理解出边长代入cosB的解析式,
解出cosB的值,从而得到角B的大小.
(Ⅱ)利用余弦定理求出ac,再根据角B的大小,代入面积公式s= ac×sinB 进行计算.
ac×sinB 进行计算.
解答:解:(Ⅰ)∵z1=z2
∴bcosC=(2a-c)cosB①,a+c=4,②(2分)
由①得2acosB=bcosC+ccosB,③(3分)
在△ABC中,由正弦定理得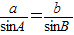 =
=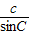 ,
,
设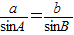 =
=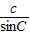 =k(k>0)
=k(k>0)
则a=ksinA,b=ksinB,c=ksinC,代入③
得; 2sinAcosB=sinBcosC+sinCcosB,(4分)
2sinAcosB=sin(B+C)=sin(π-A)=sinA (5分)
∵0<A<π∴sinA>0
∴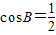 ,
,
∵0<B<π∴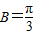 (7分)
(7分)
(Ⅱ)∵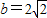 ,由余弦定理得b2=a2+c2-2accosB⇒a2+c2-ac=8,④(10分)
,由余弦定理得b2=a2+c2-2accosB⇒a2+c2-ac=8,④(10分)
由②得a2+c2+2ac=16⑤
由④⑤得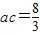 ,(12分)
,(12分)
∴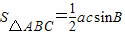 =
=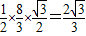 .(14分)
.(14分)
点评:本题考查复数相等的充要条件,以及利用余弦定理、正弦定理解三角形和计算三角形的面积.
解出cosB的值,从而得到角B的大小.
(Ⅱ)利用余弦定理求出ac,再根据角B的大小,代入面积公式s=
 ac×sinB 进行计算.
ac×sinB 进行计算.解答:解:(Ⅰ)∵z1=z2
∴bcosC=(2a-c)cosB①,a+c=4,②(2分)
由①得2acosB=bcosC+ccosB,③(3分)
在△ABC中,由正弦定理得
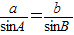 =
=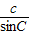 ,
,设
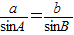 =
=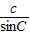 =k(k>0)
=k(k>0)则a=ksinA,b=ksinB,c=ksinC,代入③
得; 2sinAcosB=sinBcosC+sinCcosB,(4分)
2sinAcosB=sin(B+C)=sin(π-A)=sinA (5分)
∵0<A<π∴sinA>0
∴
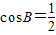 ,
,∵0<B<π∴
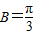 (7分)
(7分)(Ⅱ)∵
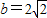 ,由余弦定理得b2=a2+c2-2accosB⇒a2+c2-ac=8,④(10分)
,由余弦定理得b2=a2+c2-2accosB⇒a2+c2-ac=8,④(10分)由②得a2+c2+2ac=16⑤
由④⑤得
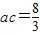 ,(12分)
,(12分)∴
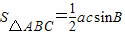 =
=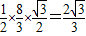 .(14分)
.(14分)点评:本题考查复数相等的充要条件,以及利用余弦定理、正弦定理解三角形和计算三角形的面积.

练习册系列答案
相关题目
 ,求△ABC的面积.
,求△ABC的面积. ,求△ABC的面积.
,求△ABC的面积. ,求△ABC的面积.
,求△ABC的面积. ,求△ABC的面积.
,求△ABC的面积.