题目内容
在进行一项掷骰子放球游戏中,规定:若掷出1点,甲盒中放一球;
若掷出2点或3点,乙盒中放一球;若掷出4点或5点或6点,丙盒中放一球,前后共掷3
次,设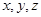 分别表示甲,乙,丙3个盒中的球数.
分别表示甲,乙,丙3个盒中的球数.
(1)求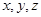 依次成公差大于0的等差数列的概率;
依次成公差大于0的等差数列的概率;
(2)记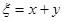 ,求随机变量
,求随机变量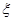 的概率分布列和数学期望.
的概率分布列和数学期望.
【答案】
(1) (2)随机变量
(2)随机变量 的概率分布列
的概率分布列
|
|
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
数学期望为
【解析】
试题分析:解:(1)x,y,z依次称公差大于0的等差数列的概率,即甲,乙,丙3个盒中的球数。
分别为0,1,2,此时的概率
(2) 的取值范围0,1,2,3,且
的取值范围0,1,2,3,且 ;
;
 ;
;
 ;
;
 .
.
随机变量 的概率分布列
的概率分布列
|
|
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
数学期望为
考点:随机变量的分布列;数学期望
点评:求随机变量的分布列和数学期望是常考题型,解决这种题目关键是求出随机变量对应的概率。

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目


 、
、 分别表示甲、乙盒子中球的个数。
分别表示甲、乙盒子中球的个数。 的概率;
的概率; 求随机变量
求随机变量 的分布列和数学期望。
的分布列和数学期望。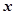 、
、 分别表示甲、乙盒子中球的个数。
分别表示甲、乙盒子中球的个数。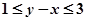 的概率;
的概率;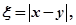 求随机变量
求随机变量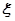 的分布列和数学期望。
的分布列和数学期望。