题目内容
下列四个说法:
(1)函数f(x)>0在x>0时是增函数,x<0也是增函数,所以f(x)是增函数;
(2)若函数f(x)=ax2+bx+2与x轴没有交点,则b2-8a<0且a>0;
(3)y=x2-2|x|-3的递增区间为[1,+∞);
(4)y=1+x和y=
表示相等函数.
其中说法正确的个数是( )
(1)函数f(x)>0在x>0时是增函数,x<0也是增函数,所以f(x)是增函数;
(2)若函数f(x)=ax2+bx+2与x轴没有交点,则b2-8a<0且a>0;
(3)y=x2-2|x|-3的递增区间为[1,+∞);
(4)y=1+x和y=
| (1+x)2 |
其中说法正确的个数是( )
| A、0 | B、1 | C、2 | D、3 |
分析:据函数在几个区间上是增函数但在区间的并集上不一定是增函数;二次函数与轴无交点等价于判别式小于0;当函数的定义域、对应法则、值域都相同时函数相同.
解答:解:对于(1),例如f(x)=-
在x>0时是增函数,x<0也是增函数;但f(x)在定义域上不是增函数.故(1)错
对于(2)函数f(x)=ax2+bx+2与x轴没有交点,则b2-8a<0或a=b=0,故(2)错
对于(3),y=x2-2|x|-3的递增区间为[1,+∞)和[-1,0],故(3)错
对于(4),y=1+x的值域为R,y=
的值域为[0,+∞),故(4)错
故选A
| 1 |
| x |
对于(2)函数f(x)=ax2+bx+2与x轴没有交点,则b2-8a<0或a=b=0,故(2)错
对于(3),y=x2-2|x|-3的递增区间为[1,+∞)和[-1,0],故(3)错
对于(4),y=1+x的值域为R,y=
| (1+x)2 |
故选A
点评:本题考查同一个函数需要定义域、对应法则、值域都相同;二次函数有根的充要条件是判别式大于等于0.

练习册系列答案
相关题目
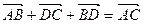 ;(2)函数
;(2)函数 是周期为
是周期为 的偶函数;(3)在
的偶函数;(3)在 中,若
中,若 ,则必有
,则必有 ;(4)把函数
;(4)把函数 的图象向左平移
的图象向左平移 个单位得到函数
个单位得到函数 的图象,其中正确说法的序号是
的图象,其中正确说法的序号是 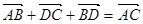 ;(2)函数
;(2)函数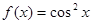 是周期为
是周期为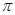 的偶函数;(3)在
的偶函数;(3)在 中,若
中,若 ,则必有
,则必有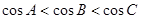 ;(4)把函数
;(4)把函数 的图象向左平移
的图象向左平移 个单位得到函数
个单位得到函数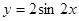 的图象,其中正确说法的序号是
的图象,其中正确说法的序号是
 表示相等函数.
表示相等函数.