题目内容
已知函数f（x）=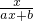
（a，b为常数，且a≠0）满足f（2）=1且方程f（x）=x有唯一解，求函数f（x）的解析式．
解：由f（2）=1，
=1，
化简得2a+b=2，又因为f（x）=x有一个解，
∴
）有唯一解
（b-1）2=0解得：a=
，b=1
当x=-
时，代入上面方程解得a=1，b=0
此时f（x）=x有唯一解
故所求为f（x）=
或f（x）=1（x≠0）
分析：先根据
=x的方程有唯一解，整理成一元二次方程，求得a和b的关系，进而根据f（2）=1求得a和b，则函数f（x）解析式可得．
点评：本题主要考查了函数与方程的综合运用．解题的过程重点根据方程得的情况判断判别式与0的关系．
=1，化简得2a+b=2，又因为f（x）=x有一个解，
∴
）有唯一解（b-1）2=0解得：a=
，b=1当x=-
时，代入上面方程解得a=1，b=0此时f（x）=x有唯一解
故所求为f（x）=
或f（x）=1（x≠0）分析：先根据
=x的方程有唯一解，整理成一元二次方程，求得a和b的关系，进而根据f（2）=1求得a和b，则函数f（x）解析式可得．点评：本题主要考查了函数与方程的综合运用．解题的过程重点根据方程得的情况判断判别式与0的关系．
练习册系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|