题目内容
已知函数f(x)在R上有定义,对任何实数a>0和任何实数x,都有f(ax)=af(x)(Ⅰ)证明f(0)=0;
(Ⅱ)证明
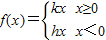 其中k和h均为常数;
其中k和h均为常数;(Ⅲ)当(Ⅱ)中的k>0时,设g(x)=
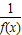 +f(x)(x>0),讨论g(x)在(0,+∞)内的单调性并求极值.
+f(x)(x>0),讨论g(x)在(0,+∞)内的单调性并求极值.
【答案】分析:(1)令x=0代入即可得到答案.
(2)分别令a=x和a=-x代入整理即可得到答案.
(3)先表示出函数g(x),然后对其进行求导,导数大于0时单调递增,导数小于0时单调递减,导数等于0时函数取到极值点.
解答:证明(Ⅰ)令x=0,则f(0)=af(0),
∵a>0,
∴f(0)=0.
(Ⅱ)①令x=a,
∵a>0,
∴x>0,则f(x2)=xf(x).
假设x≥0时,f(x)=kx(k∈R),则f(x2)=kx2,而xf(x)=x•kx=kx2,
∴f(x2)=xf(x),即f(x)=kx成立.
②令x=-a,
∵a>0,
∴x<0,f(-x2)=-xf(x)
假设x<0时,f(x)=hx(h∈R),则f(-x2)=-hx2,而-xf(x)=-x•hx=-hx2,
∴f(-x2)=-xf(x),即f(x)=hx成立.
∴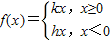 成立.
成立.
(Ⅲ)当x>0时,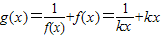 ,
,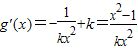
令g'(x)=0,得x=1或x=-1;
当x∈(0,1)时,g'(x)<0,∴g(x)是单调递减函数;
当x∈[1,+∞)时,g'(x)>0,∴g(x)是单调递增函数;
所以当x=1时,函数g(x)在(0,+∞)内取得极小值,极小值为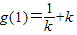
点评:本题主要考查函数的导数有关问题,当导数大于0时函数单调递增,当导数小于0时函数单调递减,当导数等于0时函数取极值点.
(2)分别令a=x和a=-x代入整理即可得到答案.
(3)先表示出函数g(x),然后对其进行求导,导数大于0时单调递增,导数小于0时单调递减,导数等于0时函数取到极值点.
解答:证明(Ⅰ)令x=0,则f(0)=af(0),
∵a>0,
∴f(0)=0.
(Ⅱ)①令x=a,
∵a>0,
∴x>0,则f(x2)=xf(x).
假设x≥0时,f(x)=kx(k∈R),则f(x2)=kx2,而xf(x)=x•kx=kx2,
∴f(x2)=xf(x),即f(x)=kx成立.
②令x=-a,
∵a>0,
∴x<0,f(-x2)=-xf(x)
假设x<0时,f(x)=hx(h∈R),则f(-x2)=-hx2,而-xf(x)=-x•hx=-hx2,
∴f(-x2)=-xf(x),即f(x)=hx成立.
∴
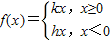 成立.
成立.(Ⅲ)当x>0时,
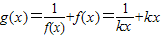 ,
,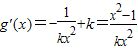
令g'(x)=0,得x=1或x=-1;
当x∈(0,1)时,g'(x)<0,∴g(x)是单调递减函数;
当x∈[1,+∞)时,g'(x)>0,∴g(x)是单调递增函数;
所以当x=1时,函数g(x)在(0,+∞)内取得极小值,极小值为
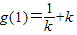
点评:本题主要考查函数的导数有关问题,当导数大于0时函数单调递增,当导数小于0时函数单调递减,当导数等于0时函数取极值点.

练习册系列答案
相关题目
已知函数f(x)在R上满足y=f(x)=2f(2-x)+ex-1+x2,则曲线y=f(x)在点(1,f(1))处的切线方程是( )
| A、2x-y-1=0 | B、x-y-3=0 | C、3x-y-2=0 | D、2x+y-3=0 |