题目内容
已知函数f(x)=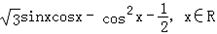 .
.
(Ⅰ) 求函数f(x)的最小值和最小正周期;
(Ⅱ)已知△ABC内角A,B,C的对边分别为a,b,c,且c=3,f(C)=0,若向量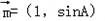 与
与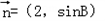 共线,求a,b的值.
共线,求a,b的值.
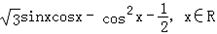 .
.(Ⅰ) 求函数f(x)的最小值和最小正周期;
(Ⅱ)已知△ABC内角A,B,C的对边分别为a,b,c,且c=3,f(C)=0,若向量
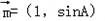 与
与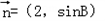 共线,求a,b的值.
共线,求a,b的值.解:(Ⅰ)函数f(x)=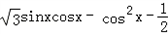 =
=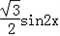 ﹣
﹣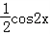 ﹣1=sin(2x﹣
﹣1=sin(2x﹣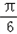 )﹣1,
)﹣1,
∴f(x)的最小值为﹣2,最小正周期为π.
(Ⅱ)∵f(C)=sin(2C﹣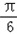 )﹣1=0,即 sin(2C﹣
)﹣1=0,即 sin(2C﹣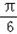 )=1,
)=1,
又∵0<C<π,﹣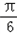 <2C﹣
<2C﹣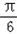 <
<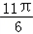 ,
,
∴2C﹣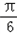 =
=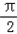 ,
,
∴C=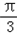 .
.
∵向量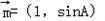 与
与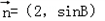 共线,
共线,
∴sinB﹣2sinA=0.
由正弦定理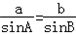 ,得 b=2a,①
,得 b=2a,①
∵c=3,由余弦定理得9=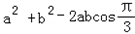 ,②
,②
解方程组①②,得 a=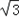 b=2
b=2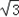 .
.
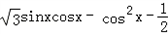 =
=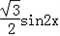 ﹣
﹣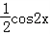 ﹣1=sin(2x﹣
﹣1=sin(2x﹣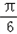 )﹣1,
)﹣1,∴f(x)的最小值为﹣2,最小正周期为π.
(Ⅱ)∵f(C)=sin(2C﹣
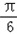 )﹣1=0,即 sin(2C﹣
)﹣1=0,即 sin(2C﹣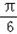 )=1,
)=1,又∵0<C<π,﹣
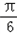 <2C﹣
<2C﹣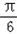 <
<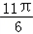 ,
,∴2C﹣
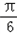 =
=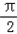 ,
,∴C=
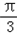 .
.∵向量
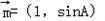 与
与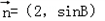 共线,
共线,∴sinB﹣2sinA=0.
由正弦定理
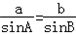 ,得 b=2a,①
,得 b=2a,①∵c=3,由余弦定理得9=
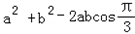 ,②
,②解方程组①②,得 a=
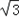 b=2
b=2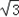 .
. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|