题目内容
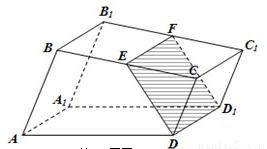
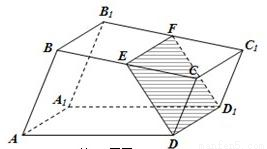
如图,已知直四棱柱ABCD—A1B=90°,AB∥DC,AB=2,AD=DC=1,AA1=2,E为BC1的中点.
(1)求证:AB1⊥BC1;
(2)若F是棱DD1上的一点,当![]() 的值为多少时,能使二面角F-AC-E为直二面角?请给出证明.
的值为多少时,能使二面角F-AC-E为直二面角?请给出证明.

解法一:(1)证明:建立如图所示的空间直角坐标系A—xyz,则依题设知
A(0,0,0),B(0,2,0),B1(0,2,![]() ),C1(1,1,
),C1(1,1,![]() ),
),
∴![]() =(0,2,
=(0,2,![]() ),
),![]() =(1,-1,
=(1,-1,![]() ). ?
). ?
∴![]() ·
·![]() =(0,2,
=(0,2,![]() )·(1,-1,
)·(1,-1,![]() )?
)?
=0×1+2×(-1)+ ![]() ×
×![]() =0. ?
=0. ?
故AB1⊥BC1. ?

(2)设F(1,0,A),∵C(1,1,0),E(![]() ,
,![]() ,
,![]() ),?
),?
∴![]() =(1,1,0),
=(1,1,0),![]() =(1,-1,0).?
=(1,-1,0).?
![]() =(
=(![]() ,
,![]() ,
,![]() )-(1,1,0)=(-
)-(1,1,0)=(-![]() ,
,![]() ,
,![]() ),?
),?
![]() =(1,1,0)-(1,0,A)=(0,1,-A),?
=(1,1,0)-(1,0,A)=(0,1,-A),?
![]() ·
·![]() =(1,1,0)·(1,-1,0)=0,
=(1,1,0)·(1,-1,0)=0,![]() ·
·![]() =(1,1,0)·(-
=(1,1,0)·(-![]() ,
,![]() ,
,![]() )=0,?
)=0,?
∴AC⊥BC,AC⊥CE. ?
若使二面角F-AC-E为直二面角,只需EC⊥FC即可,这样面FAC⊥面ACE.?
∵![]() ·
·![]() =(0,1,-A)·(-
=(0,1,-A)·(-![]() ,
,![]() ,
,![]() )=
)=![]() -
-![]() A,?
A,?
当![]() ·
·![]() =0时,得A=
=0时,得A=![]() ,即F(1,0,
,即F(1,0,![]() ), ?
), ?
故当![]() =1时,二面角F-AC-E为直二面角. ?
=1时,二面角F-AC-E为直二面角. ?
解法二:(1)证明:∵AB=2,AC=![]() =
=![]() ,∠CAB=45°, ?
,∠CAB=45°, ?
易知∠ABC=45°,∴∠ACB=90°,故AC⊥面CBB
又∵AA1=![]() ,BC=ABsin45°=
,BC=ABsin45°=![]() ,?
,?
故四边形CBB
由三垂线定理可得,AB1⊥BC1. ?

(2)∵AC⊥面CBB
∴B
?
连结A1B,A![]() =1时,二面角F-AC-E为直二面角.
=1时,二面角F-AC-E为直二面角.

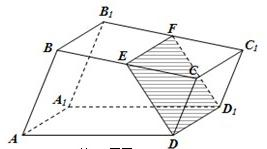 如图,已知直四棱柱ABCD-A1B1C1D1的底面是直角梯形,AB⊥BC,AB∥CD,E,F分别是棱BC,B1C1上的动点,且EF∥CC1,CD=DD1=1,AB=2,BC=3.
如图,已知直四棱柱ABCD-A1B1C1D1的底面是直角梯形,AB⊥BC,AB∥CD,E,F分别是棱BC,B1C1上的动点,且EF∥CC1,CD=DD1=1,AB=2,BC=3.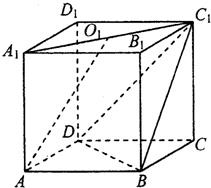 如图,已知直四棱柱ABCD-A1B1C1D1的底面边长和侧棱长均为1,且满足∠BAD=60°,O1为A1C1的中点.
如图,已知直四棱柱ABCD-A1B1C1D1的底面边长和侧棱长均为1,且满足∠BAD=60°,O1为A1C1的中点. 如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求:
如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求: