题目内容
已知f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,当x>0时,f(x)=lnx-ax.若函数f(x)在其定义域上有且仅有四个不同的零点,则实数a的取值范围是
0<a<e
0<a<e
.分析:利用函数奇偶性的对称性,只要保证x>0时,函数f(x)上有且仅有两个不同的零点即可.
解答: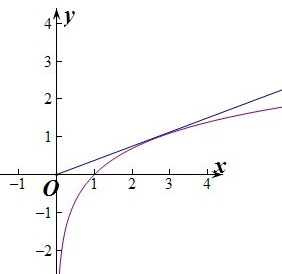 解:因为f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,
解:因为f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,
所以要使函数f(x)在其定义域上有且仅有四个不同的零点,
则只需函数f(x)在x>0上有且仅有两个不同的零点即可.
由f(x)=lnx-ax=0得lnx=ax.
设y=lnx,y=ax.
当直线y=ax与y=lnx相切时,
设切点为(x0,b),则y'=
,
则切线斜率为k=
,所以切线方程为y-lnx0=
(x-x0)=
x-1,
因为切线过原点,所以有lnx0=-1,
解得x0=
,此时k=
=e.
所以要使y=lnx与y=ax有两个不同的交点,则0<a<e.
故答案为:0<a<e.
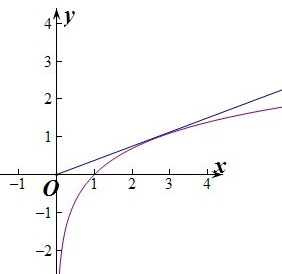 解:因为f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,
解:因为f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,所以要使函数f(x)在其定义域上有且仅有四个不同的零点,
则只需函数f(x)在x>0上有且仅有两个不同的零点即可.
由f(x)=lnx-ax=0得lnx=ax.
设y=lnx,y=ax.
当直线y=ax与y=lnx相切时,
设切点为(x0,b),则y'=
| 1 |
| x |
则切线斜率为k=
| 1 |
| x0 |
| 1 |
| x0 |
| 1 |
| x0 |
因为切线过原点,所以有lnx0=-1,
解得x0=
| 1 |
| e |
| 1 |
| x0 |
所以要使y=lnx与y=ax有两个不同的交点,则0<a<e.
故答案为:0<a<e.
点评:本题主要考查函数奇偶性的应用以及函数与方程的关系,综合性较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目