题目内容
在数列中，a1＝2，an＋1＝4an－3n＋1，n∈N*.
(1)证明数列是等比数列；
(2)求数列的前n项和Sn；
(3)证明不等式Sn＋1≤4Sn，对任意n∈N*皆成立
【答案】
(1)证明：由题设an＋1＝4an－3n＋1，得
an＋1－(n＋1)＝4(an－n)，n∈N＋.
又a1－1＝1，所以数列是首项为1，且公比为4的等比数列．
(2)由(1)可知an－n＝4n－1，于是数列的通项公式为
an＝4n－1＋n.
所以数列的前n项和Sn＝＋.
(3)证明：对任意的n∈N＋，
Sn＋1－4Sn
＝＋－4
＝－(3n2＋n－4)≤0.
所以不等式Sn＋1≤4Sn，对任意n∈N＋皆成立
【解析】略
练习册系列答案
相关题目
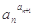为定值，则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”，且a1＝2，a2＝4，Sn为数列{an}的前n项和，则S2009＝ （ ）A.6026
B .6024 C.2
D.4