题目内容
已知函数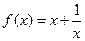
(Ⅰ)判断 的奇偶性.
的奇偶性.
(Ⅱ)判断 在
在
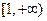 内单调性并用定义证明;
内单调性并用定义证明;
(Ⅲ)求 在区间
在区间 上的最小值.
上的最小值.
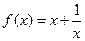
(Ⅰ)判断
 的奇偶性.
的奇偶性.(Ⅱ)判断
 在
在
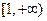 内单调性并用定义证明;
内单调性并用定义证明;(Ⅲ)求
 在区间
在区间 上的最小值.
上的最小值.(Ⅰ)  是奇函数
是奇函数
(Ⅱ) 在
在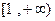 内是增函数
内是增函数
(Ⅲ)当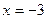
 时,
时, 有最小值为
有最小值为 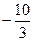
 是奇函数
是奇函数(Ⅱ)
 在
在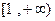 内是增函数
内是增函数(Ⅲ)当
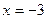
 时,
时, 有最小值为
有最小值为 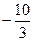
解:(1)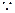
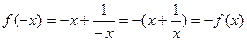

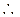
 是奇函数 ……………………………………… 3分
是奇函数 ……………………………………… 3分
(2) 在
在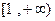 内是增函数 . ……………………………………… 5分
内是增函数 . ……………………………………… 5分
证明:设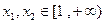 且
且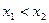
则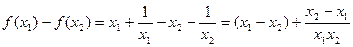 =
=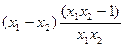
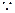
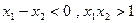
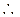
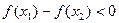 即
即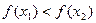
故 在
在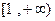 内是增函数. ………………………………………… 9分
内是增函数. ………………………………………… 9分
(3)由(1)知 是奇函数,由(2)知
是奇函数,由(2)知 在
在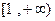 内是增函数.
内是增函数.
 在
在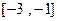 上是增函数
上是增函数
 当
当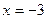
 时,
时, 有最小值为
有最小值为 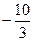 ……………………………… 12分
……………………………… 12分
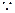
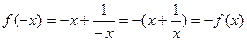

 是奇函数 ……………………………………… 3分
是奇函数 ……………………………………… 3分(2)
 在
在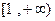 内是增函数 . ……………………………………… 5分
内是增函数 . ……………………………………… 5分证明:设
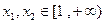 且
且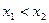
则
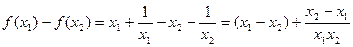 =
=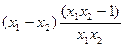
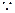
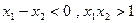
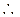
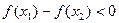 即
即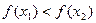
故
 在
在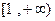 内是增函数. ………………………………………… 9分
内是增函数. ………………………………………… 9分(3)由(1)知
 是奇函数,由(2)知
是奇函数,由(2)知 在
在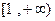 内是增函数.
内是增函数.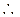
 在
在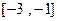 上是增函数
上是增函数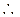 当
当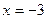
 时,
时, 有最小值为
有最小值为 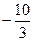 ……………………………… 12分
……………………………… 12分
练习册系列答案
相关题目
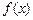 满足
满足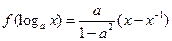 ,其中
,其中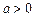 且
且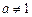 .
.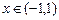 时,
时,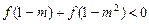 ,求实数
,求实数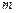 的取值集合;
的取值集合;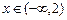 时,
时,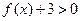 恒成立,求
恒成立,求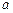 的取值范围.
的取值范围.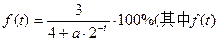 为掌握该任务的程度,t为学习时间),且这类学习任务中的某项任务满足
为掌握该任务的程度,t为学习时间),且这类学习任务中的某项任务满足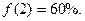
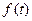 的表达式,计算
的表达式,计算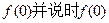 的含义;
的含义;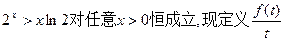 为该类学习任务在t时刻的学习效率指数,研究表明,当学习时间
为该类学习任务在t时刻的学习效率指数,研究表明,当学习时间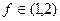 时,学习效率最佳,当学习效率最佳时,求学习效率指数相应的取值范围。
时,学习效率最佳,当学习效率最佳时,求学习效率指数相应的取值范围。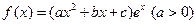 的图象在点
的图象在点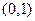 处的切线的斜率为
处的切线的斜率为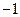 ,且在
,且在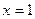 处取得极小值。
处取得极小值。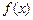 的解析式;
的解析式; 定义域为实数集
定义域为实数集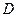 ,若存在区间
,若存在区间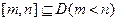 ,使得
,使得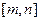 的值域也是
的值域也是 函数
函数 时,请写出函数
时,请写出函数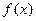 的一个“保值区间”(不必证明);
的一个“保值区间”(不必证明);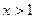 时,问
时,问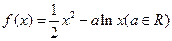
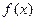 在
在 处的切线方程为
处的切线方程为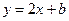 ,求
,求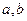 的值;
的值;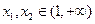 ,且
,且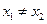 ,恒有
,恒有 ,求
,求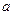 的取值范围;
的取值范围;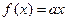 的解的个数,并说明理由。
的解的个数,并说明理由。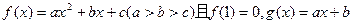
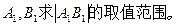
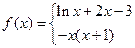
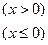 的零点个数是( )
的零点个数是( )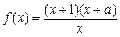 为奇函数,则
为奇函数,则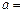 .
.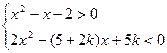 的整数解只有
的整数解只有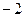 ,则实数k的取值范围是 .
,则实数k的取值范围是 .