题目内容
【题目】已知函数
.
（1）若
是函数的极值点，求
的值及函数
的极值；
（2）讨论函数的单调性.
【答案】（1）极大值为
，极小值为
；（2）见解析
【解析】（1）∵
，
∴
，
由已知
，
解得
，
此时
， 
，
当
和
时， 
， 
是增函数，
当
时， 
， 
是减函数，
所以函数
在
和
处分别取得极大值和极小值.
故函数
的极大值为
，极小值为
.
（2）由题意得
，
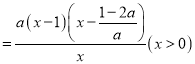①当
，即
时，
则当
时， 
， 
单调递减；
当
时， 
， 
单调递增．
②当
，即
时，
则当
和
时， 
， 
单调递增；
当
时， 
， 
单调递减．
③当
，即
时，
则当
和
时， 
， 
单调递增；
当
时， 
， 
单调递减．
④当
，即
时，
，所以
在定义域
上单调递增．
综上：①当
时， 
在区间
上单调递减，在区间
和
上单调递增；
②当
时， 
在定义域
上单调递增；
③当
时， 
在区间
上单调递减，在区间
和
上单调递增；
④当
时， 
在区间
上单调递减，在区间
上单调递增．
练习册系列答案
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案
相关题目
