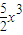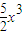题目内容
在二项式（1+x）n（n＞1，n∈N*）的展开式中，含x2项的系数记为an，则
的值为________．
2
分析：由二项式（1+x）n（n＞1，n∈N*）的展开式的通项为：Tr+1=Cnrxr可得，
，则
=
，利用裂项求和，然后求解数列的极限即可
解答：二项式（1+x）n（n＞1，n∈N*）的展开式的通项为：Tr+1=Cnrxr
令r=2可得，
∴=
∴=
=
=2
点评：本题主要考查了二项展开式的通项的应用，裂项求解数列的和及数列极限的求解，属于中档试题
分析：由二项式（1+x）n（n＞1，n∈N*）的展开式的通项为：Tr+1=Cnrxr可得，
，则=，利用裂项求和，然后求解数列的极限即可解答：二项式（1+x）n（n＞1，n∈N*）的展开式的通项为：Tr+1=Cnrxr
令r=2可得，
∴
=∴
==
=2点评：本题主要考查了二项展开式的通项的应用，裂项求解数列的和及数列极限的求解，属于中档试题
练习册系列答案
互动英语系列答案
相关题目
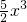
x）n的展开式中，偶数项二项式系数为32，则展开式的中间项为．
x）n的展开式中，偶数项二项式系数为32，则展开式的中间项为（ ）．
