题目内容
设数列{an}的前n项和为Sn,a1=1,an=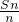 +2(n-1)(n∈N*).
+2(n-1)(n∈N*).
(1)求证:数列{an}为等差数列,并分别写出an和Sn关于n的表达式;
(2)设数列{ }的前n项和为Tn,证明:
}的前n项和为Tn,证明: ≤Tn<
≤Tn< ;
;
(3)是否存在自然数n,使得S1+ +
+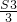 +…+
+…+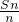 -(n-1)2=2011?若存在,求出n的值;若不存在,请说明理由.
-(n-1)2=2011?若存在,求出n的值;若不存在,请说明理由.
(1)证明:由an= +2(n-1),得Sn=nan-2n(n-1)(n∈N*).
+2(n-1),得Sn=nan-2n(n-1)(n∈N*).
当n≥2时,an=Sn-Sn-1=nan-(n-1)an-1-4(n-1),即an-an-1=4,
∴数列{an}是以a1=1为首项,4为公差的等差数列.
于是,an=4n-3,Sn═2n2-n(n∈N*).
(2)证明:∵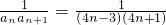 =
= ,
,
∴Tn=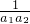 +
+ +…+
+…+ =
= [(1-
[(1- )+(
)+( -
- )+(
)+( -
- )+…+(
)+…+(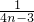 -
-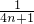 )]=
)]= (1-
(1-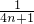 )<
)< ,
,
又易知Tn单调递增,
故Tn≥T1=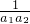 =
= ,
,
所以 ≤Tn<
≤Tn< .
.
(3)解:由Sn=nan-2n(n-1),得 =an-2(n-1)=2n-1(n∈N*),
=an-2(n-1)=2n-1(n∈N*),
∴S1+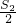 +
+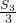 +…+
+…+ -(n-1)2=1+3+5+7+…+(2n-1)-(n-1)2
-(n-1)2=1+3+5+7+…+(2n-1)-(n-1)2
=n2-(n-1)2=2n-1.
令2n-1=2011,得n═1006,
即存在满足条件的自然数n=1006.
分析:(1)利用n≥2时,an=Sn-Sn-1,即可得到关于an与an-1的递推式,据递推式的特点可判断数列为等差数列,从而可得答案;
(2)利用裂项相消法即可求得Tn的表达式,由表达式的特点及其单调性可证;
(3)由(1)可表示出 ,进而求得S1+
,进而求得S1+ +
+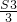 +…+
+…+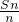 -(n-1)2,令其等于2011,看关于正整数n的方程是否有解即可;
-(n-1)2,令其等于2011,看关于正整数n的方程是否有解即可;
点评:本题考查数列的递推公式、等差数列的确定及数列与不等式的综合,考查数列求和方法,考查学生分析问题解决问题的能力,属难题,具有一定综合性.
 +2(n-1),得Sn=nan-2n(n-1)(n∈N*).
+2(n-1),得Sn=nan-2n(n-1)(n∈N*).当n≥2时,an=Sn-Sn-1=nan-(n-1)an-1-4(n-1),即an-an-1=4,
∴数列{an}是以a1=1为首项,4为公差的等差数列.
于是,an=4n-3,Sn═2n2-n(n∈N*).
(2)证明:∵
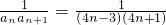 =
= ,
,∴Tn=
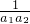 +
+ +…+
+…+ =
= [(1-
[(1- )+(
)+( -
- )+(
)+( -
- )+…+(
)+…+(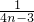 -
-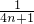 )]=
)]= (1-
(1-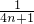 )<
)< ,
,又易知Tn单调递增,
故Tn≥T1=
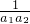 =
= ,
,所以
 ≤Tn<
≤Tn< .
.(3)解:由Sn=nan-2n(n-1),得
 =an-2(n-1)=2n-1(n∈N*),
=an-2(n-1)=2n-1(n∈N*),∴S1+
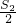 +
+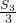 +…+
+…+ -(n-1)2=1+3+5+7+…+(2n-1)-(n-1)2
-(n-1)2=1+3+5+7+…+(2n-1)-(n-1)2=n2-(n-1)2=2n-1.
令2n-1=2011,得n═1006,
即存在满足条件的自然数n=1006.
分析:(1)利用n≥2时,an=Sn-Sn-1,即可得到关于an与an-1的递推式,据递推式的特点可判断数列为等差数列,从而可得答案;
(2)利用裂项相消法即可求得Tn的表达式,由表达式的特点及其单调性可证;
(3)由(1)可表示出
 ,进而求得S1+
,进而求得S1+ +
+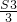 +…+
+…+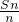 -(n-1)2,令其等于2011,看关于正整数n的方程是否有解即可;
-(n-1)2,令其等于2011,看关于正整数n的方程是否有解即可;点评:本题考查数列的递推公式、等差数列的确定及数列与不等式的综合,考查数列求和方法,考查学生分析问题解决问题的能力,属难题,具有一定综合性.

练习册系列答案
相关题目