题目内容
四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=4,BD=2
,AE,CF都与平面ABCD垂直,AE=2,CF=4.则四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据题意,先设EC与AF交与点O,过点O作OG⊥面ABCD,垂足为G;由图分析可得,四棱锥E-ABCD与四棱锥F-ABCD公共部分为四棱锥O-ABCD;根据线面垂直的性质和平面的基本性质,可得CF、OG、AE两两平行且共面;进而在平面FCAE中,计算可得OG的值,依题意,易得底面菱形ABCD的面积,由棱锥体积公式,计算可得答案.
解答: 解:根据题意,设EC与AF交与点O,过点O作OG⊥面ABCD,垂足为G;
解:根据题意,设EC与AF交与点O,过点O作OG⊥面ABCD,垂足为G;
分析可得,四棱锥E-ABCD与四棱锥F-ABCD公共部分为四棱锥O-ABCD;
依题意,AE,CF都与平面ABCD垂直,OG⊥面ABCD,
可得CF、OG、AE两两平行且共面;
又由AE=2,CF=4,
由平行线的性质,可得OG=
,
菱形中,对角线AC=4,BD=2
,可得其面积S=
×2
×4=4
,
故其体积为
×
×4
=
;
故选A.
 解:根据题意,设EC与AF交与点O,过点O作OG⊥面ABCD,垂足为G;
解:根据题意,设EC与AF交与点O,过点O作OG⊥面ABCD,垂足为G;分析可得,四棱锥E-ABCD与四棱锥F-ABCD公共部分为四棱锥O-ABCD;
依题意,AE,CF都与平面ABCD垂直,OG⊥面ABCD,
可得CF、OG、AE两两平行且共面;
又由AE=2,CF=4,
由平行线的性质,可得OG=
| 4 |
| 3 |
菱形中,对角线AC=4,BD=2
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故其体积为
| 1 |
| 3 |
| 4 |
| 3 |
| 2 |
16
| ||
| 9 |
故选A.
点评:本题考查组合体的体积计算,难点在于分析出其公共部分的形状,进而据其体积公式进行计算,要加强空间想象力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,AB为圆O的直径,点E、F在圆O上,且AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=AF=1.
如图,AB为圆O的直径,点E、F在圆O上,且AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=AF=1.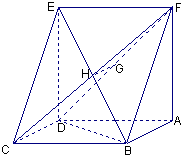 已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点. 如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点.
如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点.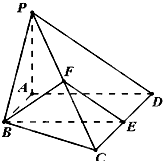 如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.
如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.