题目内容
已知2sin2α+sin2β=3sinα,则sin2α+sin2β的值域是
[0,
]∪{2}
| 5 |
| 4 |
[0,
]∪{2}
.| 5 |
| 4 |
分析:利用正弦函数的定义域、值域及其单调性和二次函数的性质即可求出.
解答:解:由2sin2α+sin2β=3sinα,及sin2β=3sinα-2sin2α得
,解得0≤sinα≤
,
或sinα=1,
∴sin2α+sin2β=-sin2α+3sinα=-(sinα-
)2+
,
∵0≤sinα≤
,或sinα=1.
∴0≤-(sinα-
)2+
≤
,或2
故sin2α+sin2β的值域是[0,
]∪{2}.
故答案为[0,
]∪{2}.
|
| 1 |
| 2 |
或sinα=1,
∴sin2α+sin2β=-sin2α+3sinα=-(sinα-
| 3 |
| 2 |
| 9 |
| 4 |
∵0≤sinα≤
| 1 |
| 2 |
∴0≤-(sinα-
| 3 |
| 2 |
| 9 |
| 4 |
| 5 |
| 4 |
故sin2α+sin2β的值域是[0,
| 5 |
| 4 |
故答案为[0,
| 5 |
| 4 |
点评:熟练掌握正弦函数的定义域、值域及其单调性和二次函数的性质是解题的关键.

练习册系列答案
相关题目
 )+2sin2
)+2sin2 .
. ,△ABC的面积S=
,△ABC的面积S= ,a=
,a= ,求sinB+sinC的值.
,求sinB+sinC的值.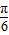 )+2sin2
)+2sin2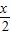 .
. ,△ABC的面积S=
,△ABC的面积S=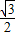 ,a=
,a=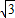 ,求sinB+sinC的值.
,求sinB+sinC的值.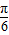 )+2sin2
)+2sin2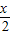 .
. ,△ABC的面积S=
,△ABC的面积S=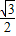 ,a=
,a=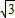 ,求sinB+sinC的值.
,求sinB+sinC的值.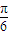 )+2sin2
)+2sin2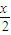 .
. ,△ABC的面积S=
,△ABC的面积S=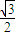 ,a=
,a=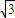 ,求sinB+sinC的值.
,求sinB+sinC的值.