题目内容
已知函数f(x)=2t2-2(ex+x)t+e2x+x2+1,g(x)=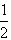 f′(x)。
f′(x)。
(1)证明:当t<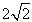 时,g(x)在R上是增函数;
时,g(x)在R上是增函数;
(2)对于给定的闭区间[a,b],试说明存在实数k,当t>k时,g(x)在闭区间[a,b]上是减函数;
(3)证明: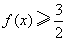 。
。
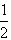 f′(x)。
f′(x)。(1)证明:当t<
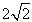 时,g(x)在R上是增函数;
时,g(x)在R上是增函数;(2)对于给定的闭区间[a,b],试说明存在实数k,当t>k时,g(x)在闭区间[a,b]上是减函数;
(3)证明:
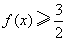 。
。解:(1)由题设得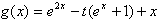 ,
,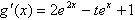
又由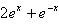 ≥
≥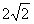 ,且t≤
,且t≤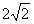 得t<
得t<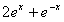
即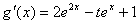 >0
>0
由此可知,g(x)为R上的增函数。
(2)因为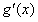 <0是g(x)为减函数的充分条件,
<0是g(x)为减函数的充分条件,
所以只要找到实数k,使得t>k时
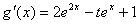 <0,即t>
<0,即t>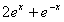 在闭区间[a,b]上成立即可
在闭区间[a,b]上成立即可
因此y=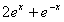 在闭区间[a,b]上连续,故在闭区[a,b]上有最大值,设其为k,
在闭区间[a,b]上连续,故在闭区[a,b]上有最大值,设其为k,
t>k时,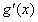 <0在闭区间[a,b]上恒成立,
<0在闭区间[a,b]上恒成立,
即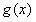 在闭区间[a,b]上为减函数。
在闭区间[a,b]上为减函数。
(3)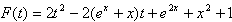
即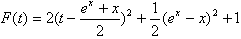
易得F(t)≥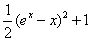
令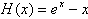 则
则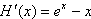
易知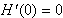
当x>0时,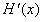 >0
>0
当x<0,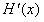 <0
<0
故当x=0时,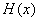 取最小值,
取最小值,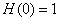
所以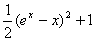 ≥
≥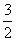 ,
,
于是对任意x、t,有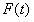 ≥
≥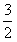 ,即
,即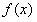 ≥
≥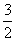 。
。
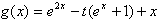 ,
,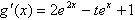
又由
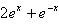 ≥
≥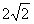 ,且t≤
,且t≤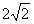 得t<
得t<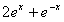
即
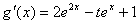 >0
>0由此可知,g(x)为R上的增函数。
(2)因为
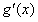 <0是g(x)为减函数的充分条件,
<0是g(x)为减函数的充分条件,所以只要找到实数k,使得t>k时
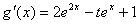 <0,即t>
<0,即t>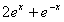 在闭区间[a,b]上成立即可
在闭区间[a,b]上成立即可因此y=
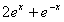 在闭区间[a,b]上连续,故在闭区[a,b]上有最大值,设其为k,
在闭区间[a,b]上连续,故在闭区[a,b]上有最大值,设其为k,t>k时,
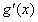 <0在闭区间[a,b]上恒成立,
<0在闭区间[a,b]上恒成立,即
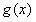 在闭区间[a,b]上为减函数。
在闭区间[a,b]上为减函数。(3)
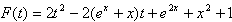
即
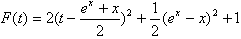
易得F(t)≥
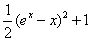
令
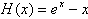 则
则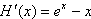
易知
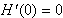
当x>0时,
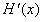 >0
>0当x<0,
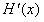 <0
<0故当x=0时,
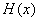 取最小值,
取最小值,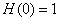
所以
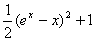 ≥
≥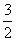 ,
,于是对任意x、t,有
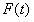 ≥
≥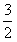 ,即
,即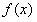 ≥
≥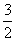 。
。
练习册系列答案
相关题目